代码随想录笔记(更新中)
Published:
数组
1. 二分查找
两种情况:左闭右闭 [left, right]、左闭右开 [left, right)
有三处不同:
- right 的初值(
right=nums.size()-1orright=nums.size()) - 循环条件(
left<=rightorleft<right) - right 的更新方式(
right=mid-1orright=mid)
左闭右闭:
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1; // 不包括右端点
while (left <= right) { // [1,1]存在(循环条件的选择考虑初始只有一个元素来判断)
int mid = (left + right) / 2;
if (nums[mid] > target)
right = mid - 1; // 子区间右闭
else if (nums[mid] < target)
left = mid + 1;
else
return mid;
}
return -1;
}
};
左闭右开:
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size(); // 包括右端点
while (left < right) { // [1,1)不存在
int mid = (left + right) / 2;
if (nums[mid] > target)
right = mid; // 子区间右开
else if (nums[mid] < target)
left = mid + 1;
else
return mid;
}
return -1;
}
};
应用:求非负整数 \(x\) 的平方根的整数部分 \([\sqrt x]\)。(69. x 的平方根)
class Solution { public: int mySqrt(int x) { int low = 0, high = x; long long mid; while (low <= high) { mid = (low + high) / 2; if (mid * mid > x) high = mid - 1; else if ((mid + 1) * (mid + 1) <= x) low = mid + 1; else break; } return (int)mid; } };
2. 移除元素(双指针)
两种经典题型:
一、移除数组 nums 中值为 val 的元素,要求时间复杂度为 O(n)。(27. 移除元素)
算法思想:用 k 记录 nums 中不等于 val 的元素个数,扫描时将不等于 val 的元素移动至下标 k - 1 的位置,并更新 k 值。扫描结束后修改数组长度。
class Solution {
public:
int removeElement(vector<int> &nums, int val) {
int k = 0; // k为不等于val的元素个数
for (int i = 0; i < nums.size(); i++) {
if (nums[i] != val) {
k++;
nums[k - 1] = nums[i];
}
}
return k;
}
};
【注】这里的 i 和 k 其实也可看作一快一慢双指针。
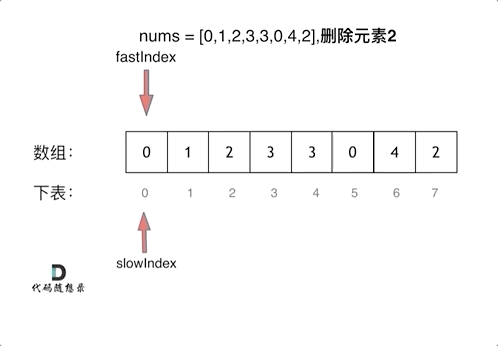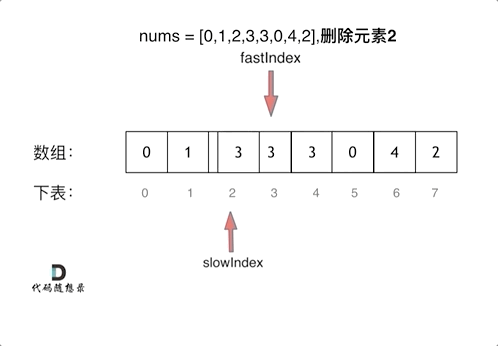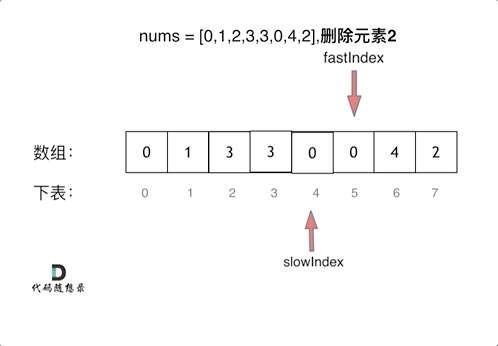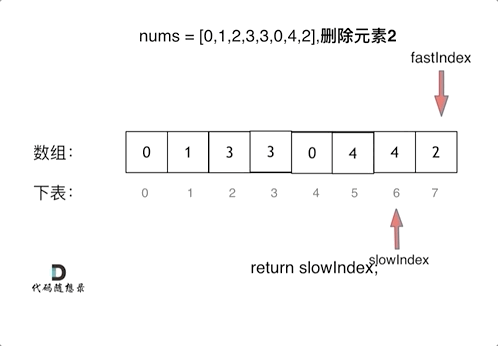
二、从有序顺序表中删除所有重复出现的元素,使每个元素只出现一次。(26. 删除有序数组中的重复项)
算法思想:使用类似于直接插入排序的思想,初始时将第一个元素视为非重复的有序表,之后依次判断后继元素是否与前面非重复有序表的最后一个元素相同。若相同,则继续向后判断;若不同,则插入前面的非重复有序表的最后,直至判断到表尾为止。(实质上也采用了双指针的思想)
class Solution {
public:
int removeDuplicates(vector<int> &nums) {
int i, j;
for (i = 0, j = 1; j < nums.size(); j++) {
// 双指针,i用于标识非重复顺序表的表尾,j是遍历数组的工作指针
if (nums[i] != nums[j])
nums[++i] = nums[j];
}
return i + 1;
}
};
3. 有序数组的平方(双指针)
对非递减序的整数数组 nums,返回由每个数字的平方组成的非递减序新数组。如输入 [-4, -1, 0, 3, 10],输出 [0, 1, 9, 16, 100]。(977.有序数组的平方)
算法思想:数组平方的最大值位于数组的两端,故考虑采用左右双指针法。
class Solution {
public:
vector<int> sortedSquares(vector<int> &nums) {
vector<int> result(nums.size());
int i = 0, j = nums.size() - 1, k = nums.size() - 1;
while (i <= j) {
if (nums[i] * nums[i] > nums[j] * nums[j]) {
result[k--] = nums[i] * nums[i];
i++;
} else {
result[k--] = nums[j] * nums[j];
j--;
}
}
return result;
}
};
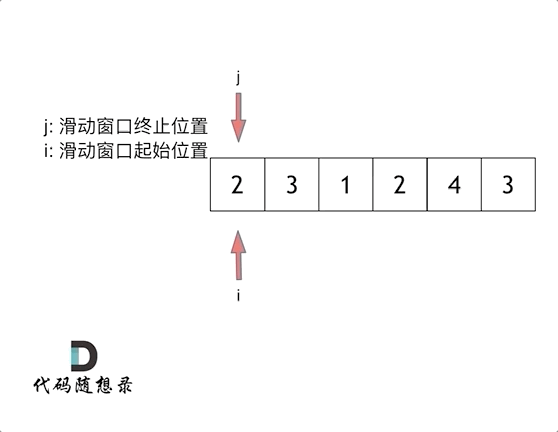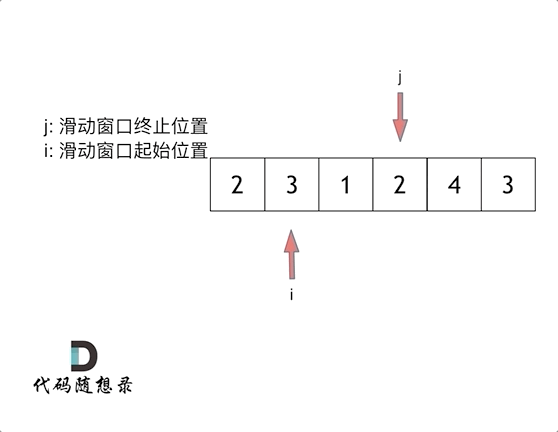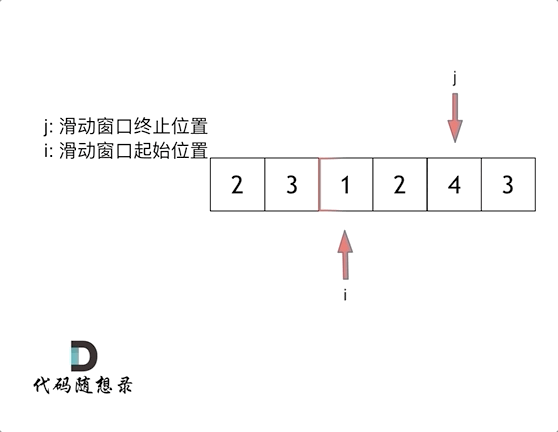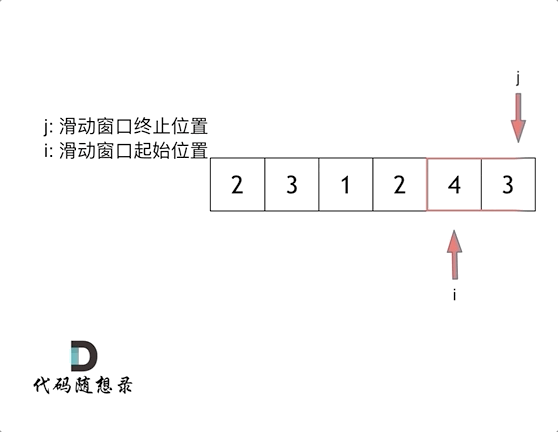
4. 长度最小的子数组(滑动窗口)※
要求:找出数组 nums 中满足元素之和 ≥s 的长度最小的连续子数组,并返回其长度。( 209.长度最小的子数组)
算法思想:滑动窗口法。对滑动窗口的终止位置进行循环遍历,滑动窗口的起始位置在当前窗口内元素之和大于等于 s 时才前移一次。
class Solution {
public:
int minSubArrayLen(int target, vector<int> &nums) {
int result = INT_MAX; // 最小子数组的长度
int sum = 0; // 滑动窗口元素值的总和
for (int i = 0, j = 0; j < nums.size(); j++) { // i,j为滑动窗口的起始位置和终止位置
sum += nums[j];
while (sum >= target) {
result = min(result, j - i + 1);
sum -= nums[i++];
}
}
return result == INT_MAX ? 0 : result;
}
};
拓展:滑动窗口 + 哈希表(904. 水果成篮)
农场种植了一排果树,用一个整数数组 fruits 表示,其中 fruits[i] 表示第 i 棵树上的水果种类。你想要尽可能多地收集水果,但是,你只有 2 个篮子,每个篮子只能装单一类型的水果,不过可装的水果总量没有限制。你可以选择任意一棵树开始连续采摘,每棵树都只摘一个水果,采摘的水果应当符合篮子中的水果类型。一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。要求返回你可以收集的水果的最大数目。例如:
输入:fruits = [3,3,3,1,2,1,1,2,3,3,4] 输出:5 解释:可以采摘 [1,2,1,1,2] 这五棵树。算法思想:使用一个滑动窗口,并保证窗口内的水果种数恒 ≤2。同时,使用一个 unordered_map 记录滑动窗口中每种水果的个数。当一个新数进入滑动窗口时,将该键对应的值加 1。若滑动窗口内的水果种数(即 unordered_map 的 size)大于2,需要将旧数移出窗口,直到窗口内的水果种数 ≤2。
class Solution { public: int totalFruit(vector<int> &fruits) { int result = 0; // 可收集水果的最大数目 unordered_map<int, int> map; // 记录滑动窗口中每种水果的个数 for (int i = 0, j = 0; j < fruits.size(); j++) { // [i,j]为滑动窗口 map[fruits[j]]++; // fruit[j]进入窗口 while (map.size() > 2) { // unordered_map获取键值对数量size是O(1)的 if (--map[fruits[i]] == 0) // fruit[i]移出窗口 map.erase(fruits[i]); i++; } result = max(result, j - i + 1); } return result; } };
5. 螺旋矩阵II(模拟,分层循环 + 边界收缩)※
生成一个包含元素 1~n2(n 为正整数)且元素按顺时针顺序螺旋排列的 n\(\times\)n 正方形矩阵。(59. 螺旋矩阵II)
算法思想:求解此类模拟题,必须坚持循环不变量原则。本题可采用分层循环法,每条边都要坚持左闭右开。
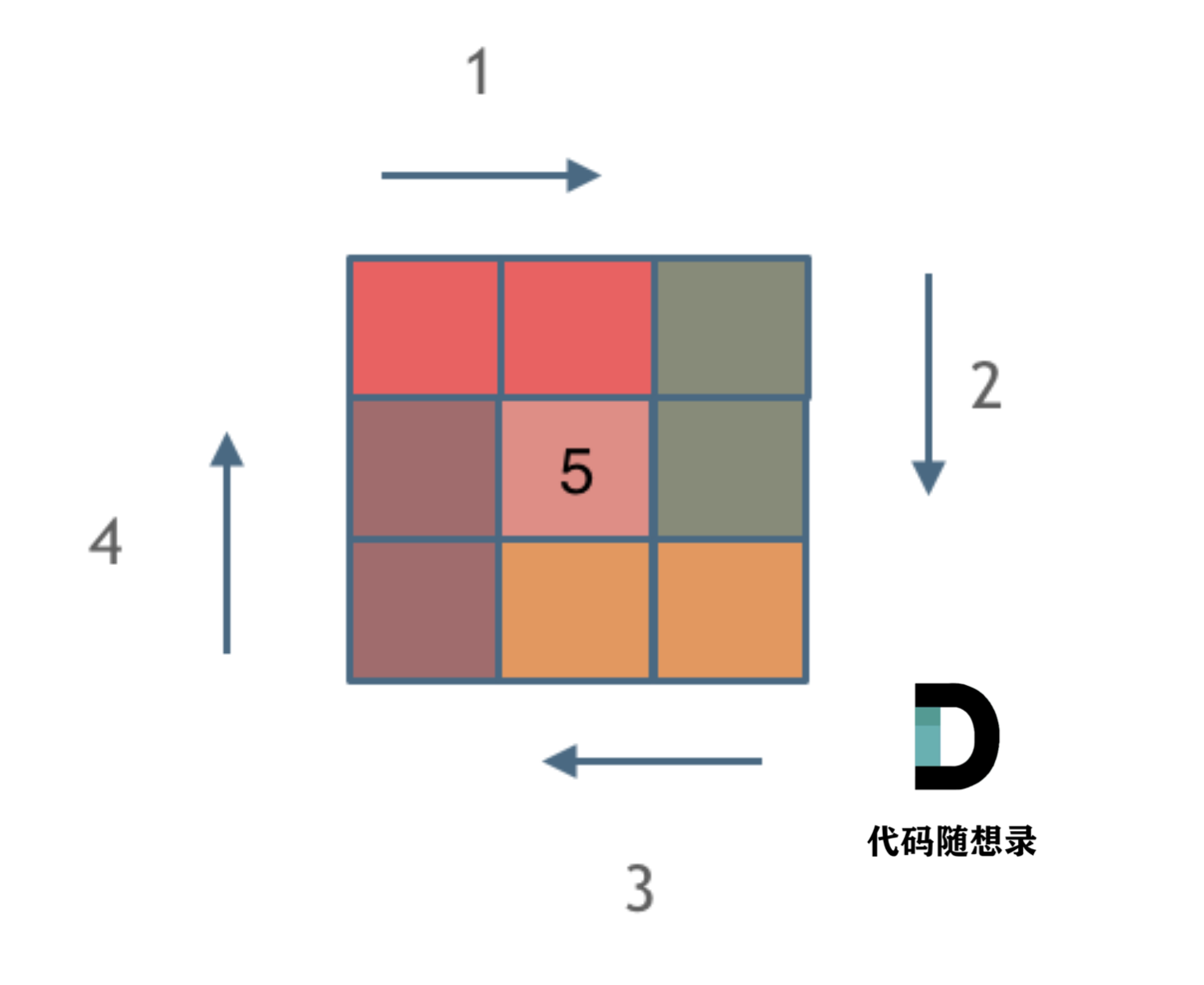
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
int k = 1;
vector<vector<int>> matrix(n, vector<int>(n));
for (int loop = 0; loop <= n / 2; loop++) { // loop表示循环次数
if (n % 2 != 0 && loop == n / 2) {
matrix[n / 2][n / 2] = k;
break;
}
for (int i = loop; i < n - 1 - loop; i++) // →
matrix[loop][i] = k++;
for (int i = loop; i < n - 1 - loop; i++) // ↓
matrix[i][n - 1 - loop] = k++;
for (int i = n - 1 - loop; i > loop; i--) // ←
matrix[n - 1 - loop][i] = k++;
for (int i = n - 1 - loop; i > loop; i--) // ↑
matrix[i][loop] = k++;
}
return matrix;
}
};
【注】也可用边界收缩法求解此类模拟问题。
考虑以下问题:按顺时针螺旋顺序返回 m\(\times\)n 矩阵的所有元素。(54. 螺旋矩阵)
由于矩阵为 m 行 n 列,若分层考虑不好下手。此时可以设置矩阵的上下左右四个边界,并在遍历过程中对边界进行收缩,算法流程如下:
- 将同一边界上的元素按顺序添加至结果列表尾部。
- 边界向内收缩 1 (代表已被打印)。
- 判断边界是否相遇(是否打印完毕),若打印完毕则跳出。
| 打印方向 | 1. 根据边界打印 | 2. 边界向内收缩 | 3. 是否打印完毕 |
|---|---|---|---|
| 从左向右 | 左边界 left → 右边界 right | 上边界 top 加 1 | 是否 top > bottom |
| 从上向下 | 上边界 top → 下边界 bottom | 右边界 right 减 1 | 是否 left > right |
| 从右向左 | 右边界 right → 左边界 left | 下边界 bottom 减 1 | 是否 top > bottom |
| 从下向上 | 下边界 bottom → 上边界 top | 左边界 left 加 1 | 是否 left > right |
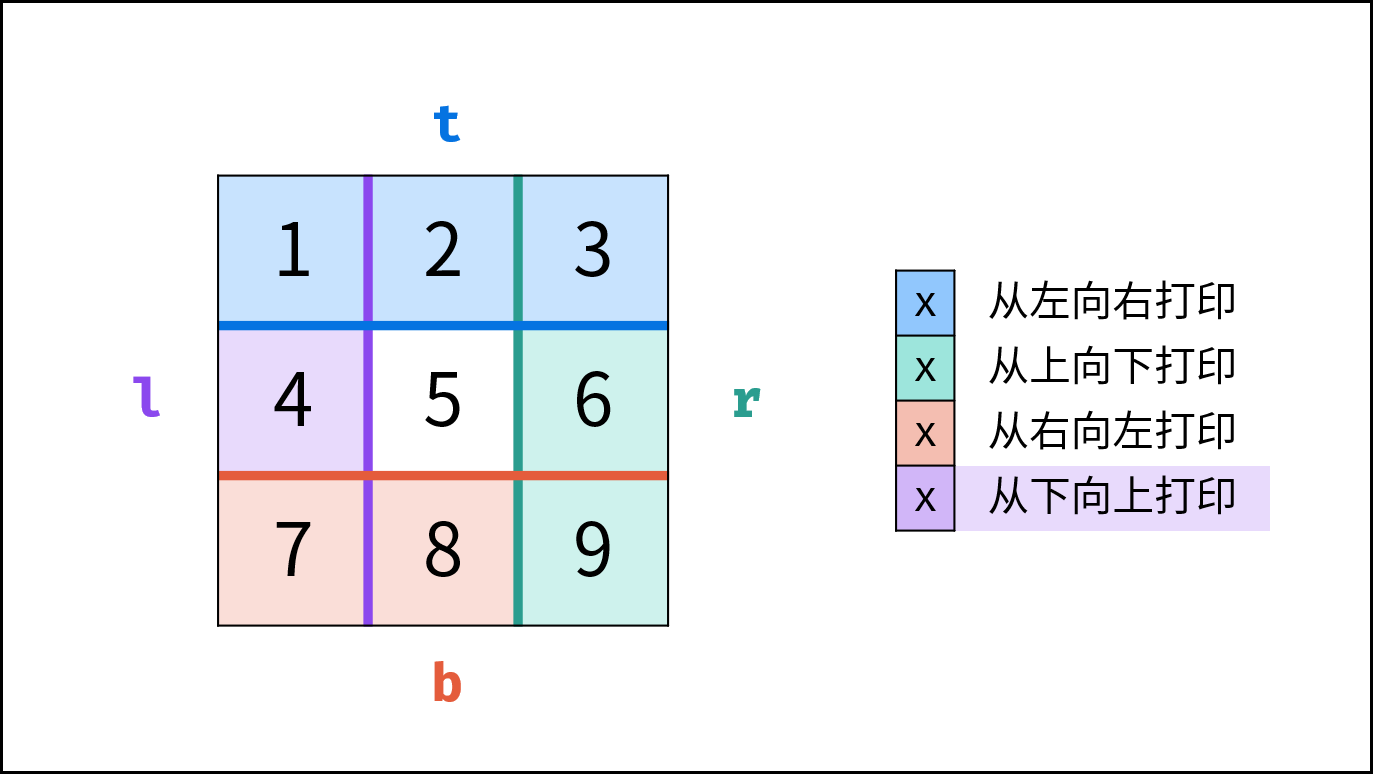
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>> &matrix) {
int m = matrix.size(), n = matrix[0].size(); // m行n列
int top = 0, bottom = m - 1, left = 0, right = n - 1; // 上下左右边界
vector<int> result;
while (true) {
for (int i = left; i <= right; i++) // →
result.push_back(matrix[top][i]);
if (++top > bottom) break;
for (int i = top; i <= bottom; i++) // ↓
result.push_back(matrix[i][right]);
if (left > --right) break;
for (int i = right; i >= left; i--) // ←
result.push_back(matrix[bottom][i]);
if (top > --bottom) break;
for (int i = bottom; i >= top; i--) // ↑
result.push_back(matrix[i][left]);
if (++left > right) break;
}
return result;
}
};
同理,59. 螺旋矩阵II也可使用边界收缩法求解:
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
int top = 0, bottom = n - 1, left = 0, right = n - 1; // 上下左右边界
int k = 1;
vector<vector<int>> matrix(n, vector<int>(n));
while (true) {
for (int i = left; i <= right; i++) // →
matrix[top][i] = k++;
if (++top > bottom) break;
for (int i = top; i <= bottom; i++) // ↓
matrix[i][right] = k++;
if (left > --right) break;
for (int i = right; i >= left; i--) // ←
matrix[bottom][i] = k++;
if (top > --bottom) break;
for (int i = bottom; i >= top; i--) // ↑
matrix[i][left] = k++;
if (++left > right) break;
}
return matrix;
}
};
6. 区间和(前缀和)※
数组的区间和表示下标 i、j 之间的元素之和,即 \(\sum\limits_{k=i}^ja[k]\)。
数组的前缀和 \(p[i]\) 表示下标 0、i 之间的元素之和,即 \(p[i]=\sum\limits_{k=0}^ia[k]\)。
区间和可由前缀和之差表示,即 \(\sum\limits_{k=i}^ja[k]=p[j]-p[i-1]\)。
通过数组的前缀和列表,可以高效地求解涉及区间和的问题。(58. 区间和 - 卡码网KamaCoder)
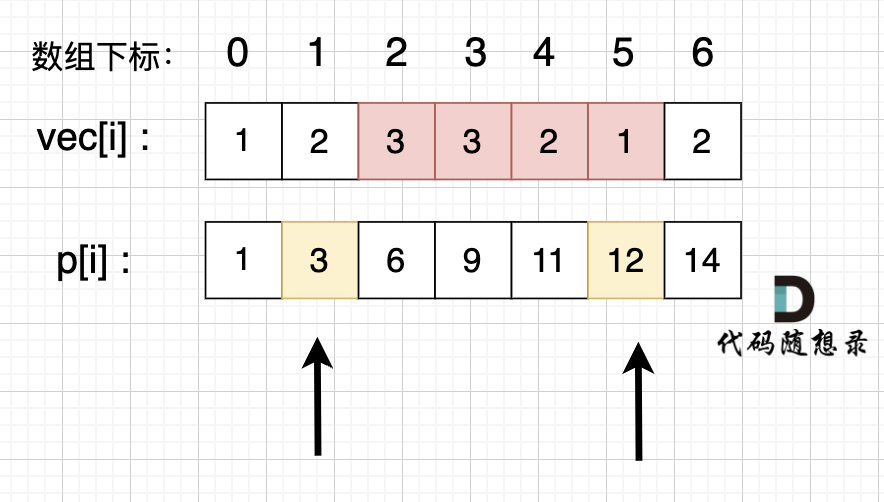
class Solution {
public:
void intervalSum() {
int n, a, b, sum = 0;
cin >> n; // 输入数组长度
vector<int> Array(n), prefix(n); // prefix为前缀和列表
for (int i = 0; i < n; i++) {
cin >> Array[i]; // 输入数组元素
sum += Array[i];
prefix[i] = sum;
}
while (cin >> a >> b) // 输入指定区间[a,b]
cout << (a == 0 ? prefix[b] : prefix[b] - prefix[a - 1]) << endl; // 输出对应的区间和
}
};
【注】在上面的实现中,当区间的左端点下标是 0 时,需要特判。因此,前缀和的另一种定义中规定 \(p[0]=0\),于是有 \(p[1]=a[0], p[2]=a[1],..., p[i+1]=\sum\limits_{k=0}^{i}a[k]\)。从而 \(a[i]\) 到 \(a[j]\) 之间的元素和为 \(p[j+1]-p[i]\) (相当于下标从 1 开始)。此外,定义 \(p[0]=0\) 也可以兼容 \(a\) 为空数组的情况。
原数组a: [1 2 3 4 5] 前缀和数组p: [0 1 3 6 10 15]class NumArray { vector<int> p; // 前缀和数组 public: NumArray(vector<int> &nums) { p.resize(nums.size() + 1); for (int i = 0; i < nums.size(); i++) p[i + 1] = p[i] + nums[i]; } int sumRange(int left, int right) { return p[right + 1] - p[left]; } };
【扩展】各类区间求和问题解法(详解)
- 数组不变,区间查询:前缀和、树状数组、线段树;
- 数组单点修改,区间查询:树状数组、线段树;
- 数组区间修改,单点查询:差分、线段树;
- 数组区间修改,区间查询:线段树。
7. 开发商购买土地(二维前缀和)※
类似于一维数组前缀和的思想,二维前缀和数组 \(p[i][j]\) 表示原二维数组 \(a\) 中以 \(a_{11}\) 为左上角、\(a_{ij}\) 为右下角的子矩阵的元素和(注意,在计算二维前缀和数组时,下标从 1 开始)。
原数组a:
1 2 3
4 5 6
7 8 9
二维前缀和数组p:
0 0 0 0
0 1 3 6
0 5 12 21
0 12 27 45
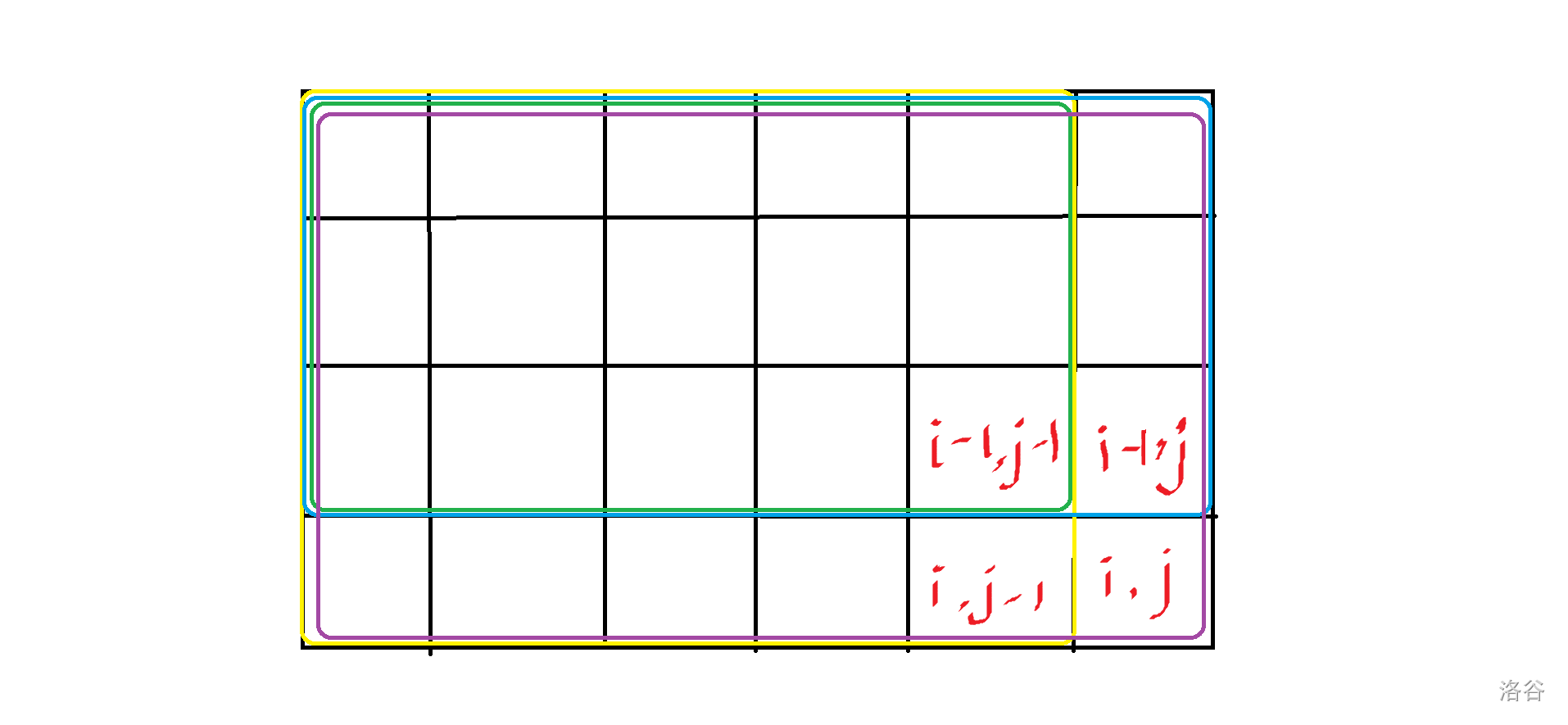
显然,计算 \(p[i][j]\) 的递推公式为:\(p[i][j]=p[i-1][j]+p[i][j-1]-p[i-1][j-1]+a_{ij}\),不难写出对应代码:
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
p[i][j] = p[i - 1][j] + p[i][j - 1] - p[i - 1][j - 1] + A[i - 1][j - 1]; //注意下标
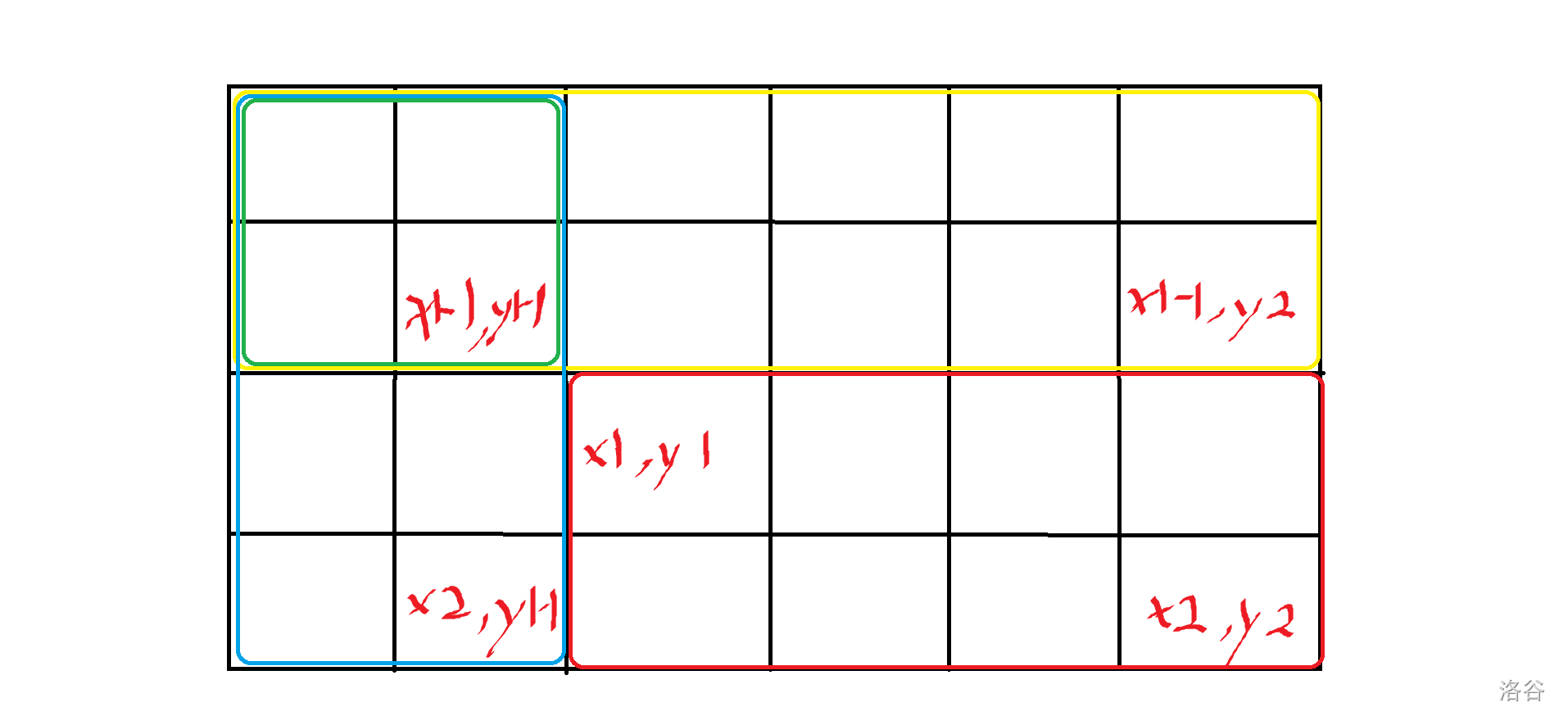
得到二维前缀和数组后,可求得以 \(a_{x_1,y_1}\) 为左上角、\(a_{x_2,y_2}\) 为右下角的子矩阵元素和为\(p[x_2][y_2]-p[x_1-1][x_2]-p[x_2][y_1-1]+p[x_1-1][y_1-1]\)。查询的操作是 O(1) 的,大大提高了效率。
以44. 开发商购买土地 - 卡码网KamaCoder为例,本题要求找到一个横向或纵向划分,将一个 n\(\times\)m 矩阵划分为两个子矩阵,使得两子矩阵的元素和之间的差距最小。显然,该题涉及到子矩阵元素和的计算,用二维前缀和很合适。
class Solution {
public:
int minGap() {
int n, m, x, result = INT32_MAX;
cin >> n >> m; // n行m列
vector<vector<int>> p(n + 1, vector<int>(m + 1)); // 二维前缀和列表
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
cin >> x;
p[i][j] = p[i - 1][j] + p[i][j - 1] - p[i - 1][j - 1] + x;
}
for (int i = 1; i < n; i++) // 横向划分
result = min(result, abs(2 * p[i][m] - p[n][m]));
for (int j = 1; j < m; j++) // 纵向划分
result = min(result, abs(2 * p[n][j] - p[n][m]));
return result;
}
};
class NumMatrix { vector<vector<int>> p; public: NumMatrix(vector<vector<int>> &matrix) { p.resize(matrix.size() + 1); for (int i = 0; i <= matrix.size(); i++) p[i].resize(matrix[0].size() + 1); // 将二维前缀和数组resize为指定大小 for (int i = 1; i <= matrix.size(); i++) for (int j = 1; j <= matrix[0].size(); j++) p[i][j] = p[i - 1][j] + p[i][j - 1] - p[i - 1][j - 1] + matrix[i - 1][j - 1]; } int sumRegion(int row1, int col1, int row2, int col2) { return p[row2 + 1][col2 + 1] - p[row1][col2 + 1] - p[row2 + 1][col1] + p[row1][col1]; } };
8. 总结
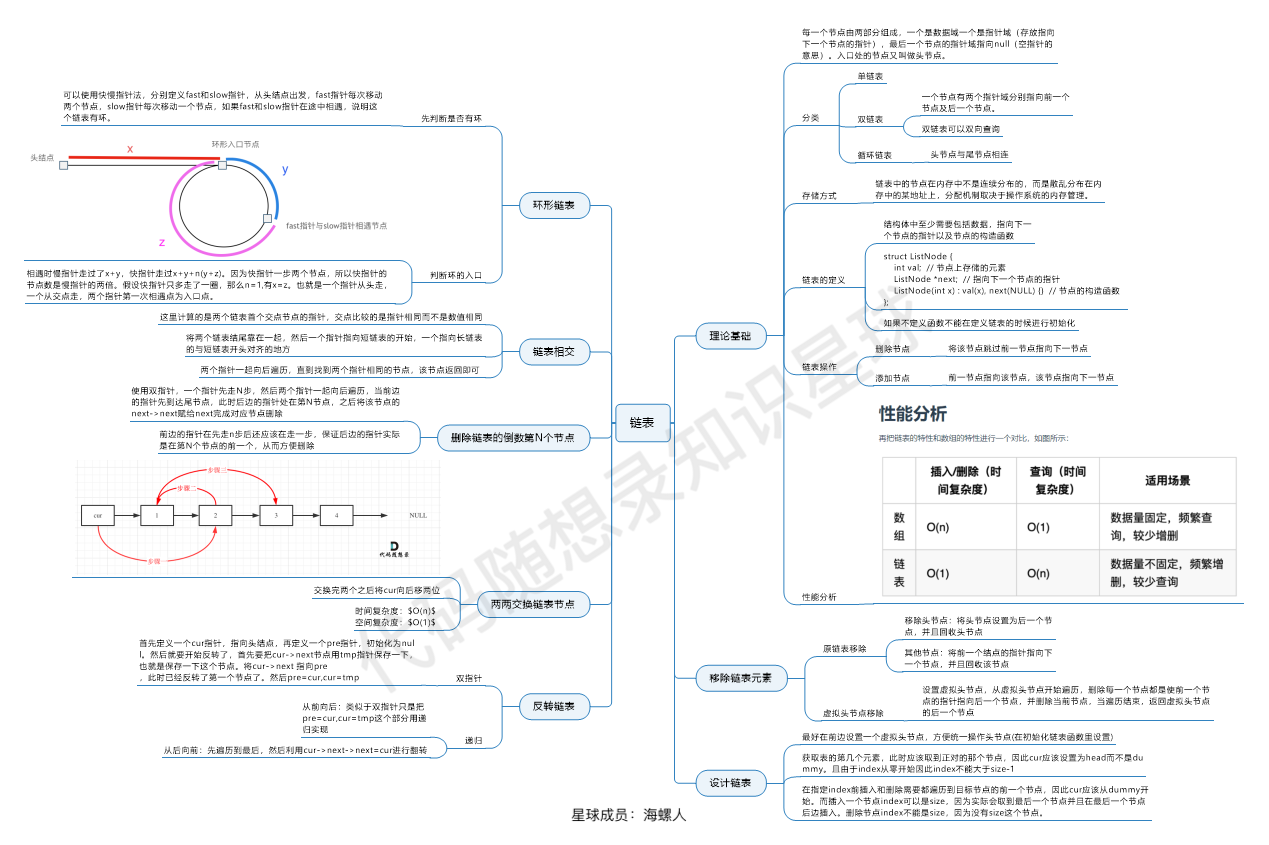
链表
LeetCode 对单链表的定义:
struct ListNode { int val; ListNode *next; ListNode() : val(0), next(nullptr) {} ListNode(int x) : val(x), next(nullptr) {} ListNode(int x, ListNode *next) : val(x), next(next) {} };对双链表的定义:
struct DListNode { int val; DListNode *prev, *next; DListNode() : val(0), prev(nullptr), next(nullptr) {} DListNode(int x) : val(x), prev(nullptr), next(nullptr) {} DListNode(int x, DListNode *prev, DListNode *next) : val(x), prev(prev), next(next) {} };
1. 移除链表元素
删除单链表中所有数据域为 val 的结点。(203. 移除链表元素)
class Solution {
public:
ListNode *removeElements(ListNode *head, int val) {
ListNode *dummyHead = new ListNode(0, head); // 虚拟头结点
ListNode *p = dummyHead;
while (p->next != nullptr) {
if (p->next->val == val) {
ListNode *q = p->next;
p->next = q->next;
delete q;
} else
p = p->next;
}
return dummyHead->next;
}
};
2. 设计链表
使用单链表或双链表设计一个类实现自己的链表。(707. 设计链表)
- 单链表:
class MyLinkedList {
public:
MyLinkedList() { // 初始化 MyLinkedList 对象
this->head = new ListNode(0);
this->size = 0;
}
int get(int index) { // 获取链表中下标为 index 的节点的值
if (index < 0 || index >= this->size)
return -1;
ListNode *p = this->head;
for (int i = 0; i <= index; i++)
if (p->next != nullptr)
p = p->next;
return p->val;
}
void addAtHead(int val) { // 将一个值为 val 的节点插入到链表中第一个元素之前
ListNode *p = new ListNode(val, this->head->next);
this->head->next = p;
this->size++;
}
void addAtTail(int val) { // 将一个值为 val 的节点追加到链表中作为链表的最后一个元素
ListNode *p = this->head, *q = new ListNode(val);
while (p->next != nullptr)
p = p->next;
p->next = q;
this->size++;
}
void addAtIndex(int index, int val) { // 将一个值为 val 的节点插入到链表中下标为 index 的节点之前
if (index < 0 || index > this->size)
return;
ListNode *p = this->head;
for (int i = 0; i < index; i++)
if (p->next != nullptr)
p = p->next;
ListNode *q = new ListNode(val, p->next);
p->next = q;
this->size++;
}
void deleteAtIndex(int index) { // 删除链表中下标为 index 的节点
if (index < 0 || index >= this->size)
return;
ListNode *p = this->head;
for (int i = 0; i < index; i++)
if (p->next != nullptr)
p = p->next;
ListNode *q = p->next;
p->next = q->next;
delete q;
this->size--;
}
private:
ListNode *head; // 头结点
int size; // 链表长度
};
- 双链表:
class MyLinkedList {
public:
MyLinkedList() { // 初始化 MyLinkedList 对象
this->head = new DListNode(0);
this->size = 0;
}
int get(int index) { // 获取链表中下标为 index 的节点的值
if (index < 0 || index >= this->size)
return -1;
DListNode *p = this->head;
for (int i = 0; i <= index; i++)
if (p->next != nullptr)
p = p->next;
return p->val;
}
void addAtHead(int val) { // 将一个值为 val 的节点插入到链表中第一个元素之前
DListNode *p = new DListNode(val, this->head, this->head->next);
if (this->head->next != nullptr)
this->head->next->prev = p;
this->head->next = p;
this->size++;
}
void addAtTail(int val) { // 将一个值为 val 的节点追加到链表中作为链表的最后一个元素
DListNode *p = this->head, *q = new DListNode(val);
while (p->next != nullptr)
p = p->next;
p->next = q;
q->prev = p;
this->size++;
}
void addAtIndex(int index, int val) { // 将一个值为 val 的节点插入到链表中下标为 index 的节点之前
if (index < 0 || index > this->size)
return;
DListNode *p = this->head;
for (int i = 0; i < index; i++)
if (p->next != nullptr)
p = p->next;
DListNode *q = new DListNode(val, p, p->next);
if (p->next != nullptr)
p->next->prev = q;
p->next = q;
this->size++;
}
void deleteAtIndex(int index) { // 删除链表中下标为 index 的节点
if (index < 0 || index >= this->size)
return;
DListNode *p = this->head;
for (int i = 0; i < index; i++)
if (p->next != nullptr)
p = p->next;
DListNode *q = p->next;
if (q->next != nullptr)
q->next->prev = p;
p->next = q->next;
delete q;
this->size--;
}
private:
DListNode *head; // 头结点
int size; // 链表长度
};
3. 翻转链表(头插法 + 双指针法)
方法一:头插法(206. 反转链表)
class Solution {
public:
ListNode *reverseList(ListNode *head) {
ListNode *dummyHead = new ListNode(0);
ListNode *p = head, *r;
while (p != nullptr) {
r = p->next; // 暂存p的后继结点
p->next = dummyHead->next;
dummyHead->next = p; // 将p插入头结点之后
p = r;
}
return dummyHead->next;
}
};
方法二:双指针法——反转指针朝向
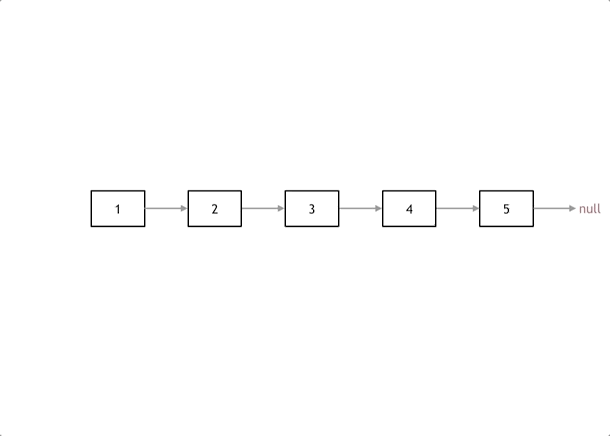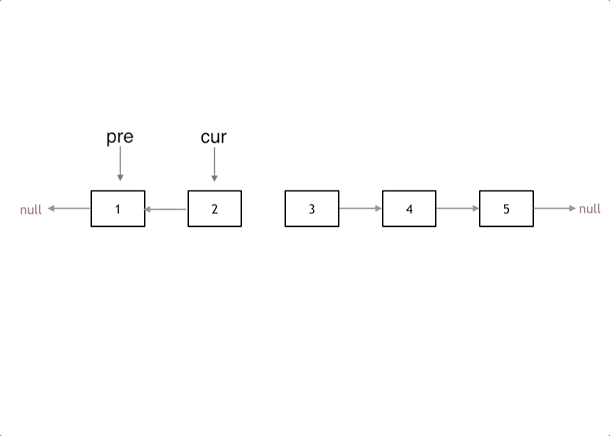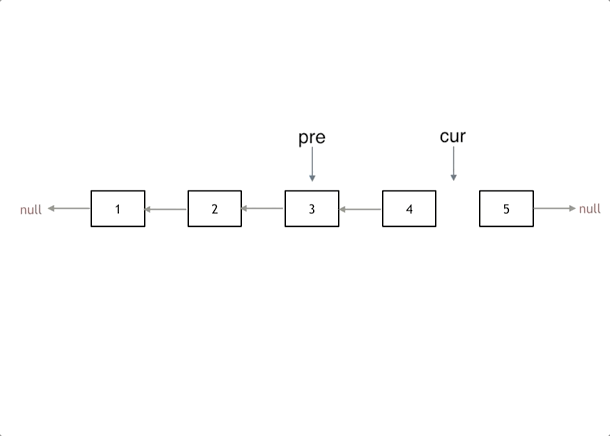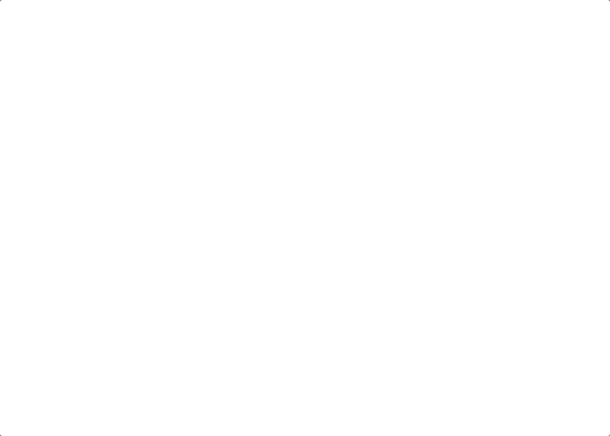
class Solution {
public:
ListNode *reverseList(ListNode *head) {
ListNode *pre = nullptr, *cur = head;
while (cur != nullptr) {
ListNode *temp = cur->next; // 暂存cur的后继结点
cur->next = pre; // 改变指针朝向
pre = cur;
cur = temp; // pre和cur依次右移
}
return pre;
}
};
4. 两两交换链表中的结点
要求两两交换链表中相邻的结点。如 [1, 2, 3, 4] → [2, 1, 4, 3]。(24. 两两交换链表中的节点)
class Solution {
public:
ListNode *swapPairs(ListNode *head) {
ListNode *dummyHead = new ListNode(0, head);
ListNode *p = dummyHead;
while (p->next != nullptr && p->next->next != nullptr) {
ListNode *q = p->next->next;
p->next->next = q->next;
q->next = p->next;
p->next = q;
p = q->next;
}
return dummyHead->next;
}
};
5. 删除链表的倒数第N个结点(快慢双指针)
class Solution {
public:
ListNode *removeNthFromEnd(ListNode *head, int n) {
ListNode *dummyHead = new ListNode(0, head);
ListNode *p = dummyHead, *q = dummyHead; // 快慢双指针
while (n--)
p = p->next; // p先右移n次
while (p->next != nullptr) {
p = p->next;
q = q->next; // p和q同步右移,结束后q指向待删除结点的前驱结点
}
ListNode *r = q->next;
q->next = r->next;
delete r;
return dummyHead->next;
}
};
6. 链表相交(双指针)
返回两个单链表相交的起始节点。(160. 相交链表)
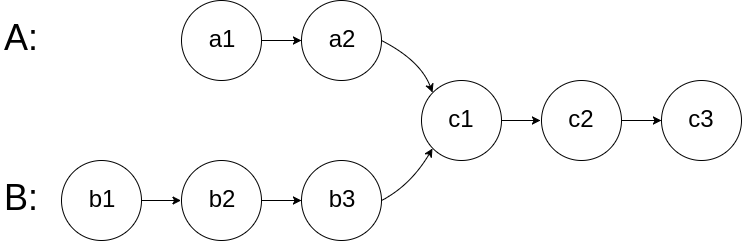
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0, lenB = 0; // headA和headB的长度
ListNode *p, *q;
for (p = headA; p != nullptr; p = p->next)
lenA++;
for (q = headB; q != nullptr; q = q->next)
lenB++;
p = headA;
q = headB;
if (lenA > lenB)
for (int i = 0; i < lenA - lenB; i++)
p = p->next;
else if (lenA < lenB)
for (int j = 0; j < lenB - lenA; j++)
q = q->next;
while (p != q) {
p = p->next;
q = q->next;
}
return p;
}
};
7. 环形链表II(快慢双指针)※
要求:单链表有环,是指单链表的最后一个结点的指针指向了链表中的某个结点。 判断单链表是否存在环,若有环,则返回链表开始入环的第一个结点。(142. 环形链表II)
算法思想:
设置快慢双指针 fast 和 slow ,最初都指向链表头 head。slow 每次走一步,fast 每次走两步。fast 比 slow 走得快,故若有环,则 fast 一定比 slow 先进入环。入环后,两个指针一定能在环上相遇。这样就可以判断一个链表是否有环。
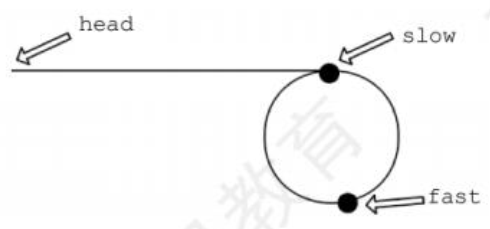
- 当 slow 刚进入环时,fast 早已进入环。因为 fast 每次比 slow 多走一步且 fast 与 slow 的距离小于环的长度,所以 fast 与 slow 相遇时,slow 所走的距离不超过环的长度。
设表头到环的入口点的距离为 a,环的入口点到相遇点的距离为 x,环长为 r,相遇时 fast 绕过了 n 圈,则有 \(2(a+x)=a+nr+x\),即 \(a=nr-x\)。因此可设置两个指针,一个指向 head,一个指向相遇点,两个指针同步移动 (均为一次走一步),相遇点即为环的入口点。
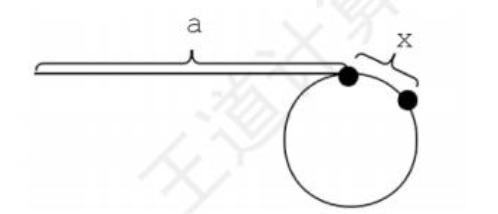
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast = head, *slow = head; // 快慢双指针
while (fast != nullptr && fast->next != nullptr) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast)
break;
}
if (fast == nullptr || fast->next == nullptr)
return nullptr;
ListNode *p = head, *q = fast; // 分别指向表头和相遇点
while (p != q) {
p = p->next;
q = q->next;
}
return p; // 返回入口点
}
};
8. 总结
哈希表
当遇到要快速判断一个元素是否出现在集合中的问题时,就要考虑哈希法。
使用哈希法解决问题时,一般会选择如下三种数据结构:数组、集合(set)、映射(map)。
集合 底层实现 是否有序 数值是否可以重复 能否更改数值 查询效率 增删效率 std::set 红黑树 有序 否 否 O(log n) O(log n) std::multiset 红黑树 有序 是 否 O(log n) O(log n) std::unordered_set 哈希表 无序 否 否 O(1) O(1)
映射 底层实现 是否有序 数值是否可以重复 能否更改数值 查询效率 增删效率 std::map 红黑树 key有序 key不可重复 key不可修改 O(log n) O(log n) std::multimap 红黑树 key有序 key可重复 key不可修改 O(log n) O(log n) std::unordered_map 哈希表 key无序 key不可重复 key不可修改 O(1) O(1) 例如,当我们要使用集合来解决哈希问题的时候,优先使用 unordered_set,因为它的查询和增删效率是最优的;如果需要集合是有序的,那么就用 set;如果要求不仅有序还要有重复数据的话,那么就用 multiset。
【注】数组、unordered_set、unordered_map 实现的对比:
- 数组:适用于键为可控范围整数或字符、统计频率或存在性的场景,性能最好。(键稀疏时,使用数组会浪费内存。如果题目未限制键的范围,就不能用数组来做哈希表)
- unordered_set:适用于仅需存储唯一键(去重)、快速查询存在性且无需关联值的场景。(若键是复杂类型,需自定义哈希函数)
- unordered_map:适用于键值对映射(如数组下标、词频统计)、对键哈希的场景。
1. 有效的字母异位词(数组)※
要求:判断两个字符串 s 和 t 是否互为字母异位词(重新排列源单词的所有字母得到的一个新单词),字符串只包括小写字母。(242. 有效的字母异位词)
算法思路:
- 定义一个数组 record,记录字符串 s 中字符 'a'~'z' 出现的次数(将 ‘a’~’z’ 映射为下标 0~25)。
- 遍历字符串 s 时,对
record[s[i]-'a']做 +1 操作;遍历字符串 t 时,对record[t[i]-'a']做 -1 操作。若 s 和 t 互为字母异位词,record中的元素最终为全0。

class Solution {
public:
bool isAnagram(string s, string t) {
int record[26] = {0}; // 记录s中每个字符出现的次数
for (int i = 0; i < s.size(); i++)
record[s[i] - 'a']++;
for (int i = 0; i < t.size(); i++)
record[t[i] - 'a']--;
for (int i = 0; i < 26; i++)
if (record[i] != 0)
return false;
return true;
}
};
拓展:哈希表 + 滑动窗口
要求:找到字符串 s 中所有是单词 p 的异位词的子串,返回这些子串的起始索引。(438. 找到字符串中所有字母异位词)
算法思想:使用一个与单词 p 大小相同的滑动窗口,分别用一个数组维护单词 p 和滑动窗口中的字符频率。窗口在 s 上滑动时,对移入的新字符进行“+1”操作,对移出的旧字符进行“-1”操作,若某时刻两数组各字符频率均相同,此时的滑动窗口就是一个满足条件的子串。
class Solution { public: vector<int> findAnagrams(string s, string p) { vector<int> pRecord(26, 0), windowRecord(26, 0), result; if (s.size() < p.size()) return result; for (int i = 0; i < p.size(); i++) { pRecord[p[i] - 'a']++; // 记录p中的字符频率 windowRecord[s[i] - 'a']++; // 记录初始滑动窗口的字符频率 } if (pRecord == windowRecord) // 判断初始滑动窗口是否满足异位词 result.push_back(0); for (int j = p.size(); j < s.size(); j++) { windowRecord[s[j] - 'a']++; // 新字符移入滑动窗口 windowRecord[s[j - p.size()] - 'a']--; // 窗口中的首字符移出滑动窗口 if (pRecord == windowRecord) result.push_back(j - p.size() + 1); } return result; } };
2. 两个数组的交集(unordered_set + 数组)※
返回两个数组的交集,要求输出结果中每个元素均唯一且不用考虑输出结果的顺序。(349. 两个数组的交集)
解法一:使用 unordered_set 作哈希表。
class Solution {
public:
vector<int> intersection(vector<int> &nums1, vector<int> &nums2) {
unordered_set<int> result, s(nums1.begin(), nums1.end()); // vector转unordered_set
for (int x : nums2)
if (s.find(x) != s.end())
result.insert(x);
return vector<int>(result.begin(), result.end()); // unordered_set转vector
}
};
解法二:使用数组作哈希表。(0 <= nums1[i], nums2[i] <= 1000)
class Solution {
public:
vector<int> intersection(vector<int> &nums1, vector<int> &nums2) {
vector<bool> record(1001, false);
unordered_set<int> result;
for (int x : nums1)
record[x] = true;
for (int y : nums2)
if (record[y] == true)
result.insert(y);
return vector<int>(result.begin(), result.end());
}
};
【注】若输出结果不去重,解法如下:(350. 两个数组的交集 II)
class Solution { public: vector<int> intersect(vector<int> &nums1, vector<int> &nums2) { vector<int> record(1001, 0), result; for (int x : nums1) record[x]++; for (int y : nums2) if (record[y] > 0) { result.push_back(y); record[y]--; } return result; } };
3. 快乐数(unordered_set)
判断一个数 n 是不是快乐数。(202. 快乐数)
“快乐数”定义为:
· 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
· 然后重复这个过程直到这个数变为1,也可能是无限循环但始终变不到1。
· 如果这个过程结果为1,那么这个数就是快乐数。
例如:
输入:n = 19
输出:true
解释:
1² + 9² = 82
8² + 2² = 68
6² + 8² = 100
1² + 0² + 0² = 1
算法思想:若一个数不是快乐数,则重复该过程会无限循环,即一定有一个中间和数会重复出现。因此,可以用一个 unordered_set 记录求得的中间和数,若某一轮求得的和数已在该哈希表中,则该数不是快乐数。
class Solution {
public:
bool isHappy(int n) {
unordered_set<int> s;
while (n != 1) {
int sum = 0;
while (n > 0) { // 求和数
sum += (n % 10) * (n % 10);
n /= 10;
}
if (s.find(sum) != s.end()) // 和数重复出现,一定无限循环
return false;
s.insert(sum);
n = sum;
}
return true;
}
};
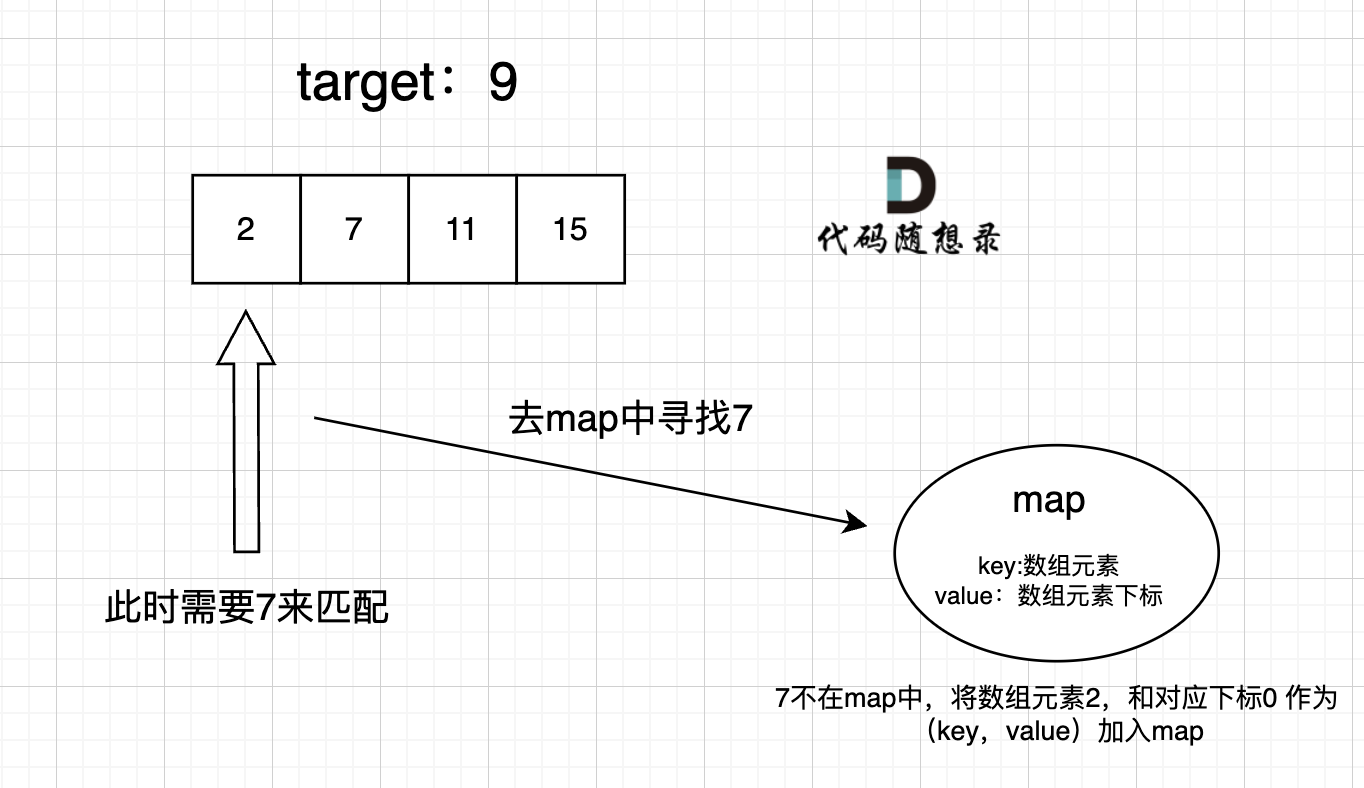
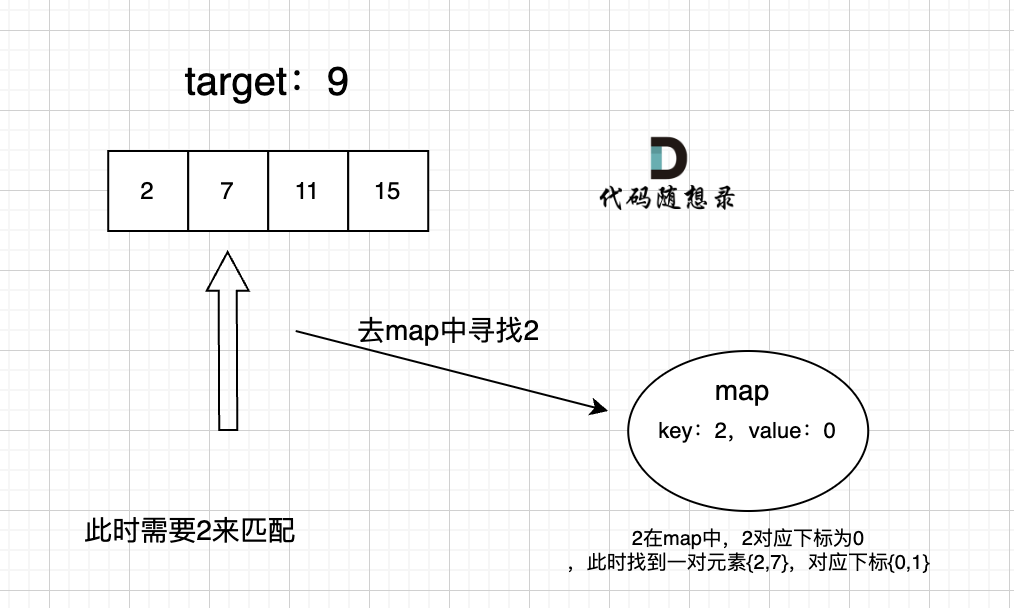
4. 两数之和(unordered_map)※
在整数数组 nums 中找出和为目标值 target 的两个整数,并返回它们的数组下标。假设只存在一个有效答案,且可以按任意顺序返回答案。(1. 两数之和)
算法思想:由于题目要求返回下标,且不要求输出结果有序,可以使用 unordered_map 记录在遍历数组时已经访问过的元素, key 保存数组元素、value 保存数组元素的下标。这样,每访问一个元素 num,检查键 target - num 是否已在哈希表中,若在,则返回二者的下标;否则将该元素及其下标存入哈希表,继续遍历。
class Solution {
public:
vector<int> twoSum(vector<int> &nums, int target) {
unordered_map<int, int> map; // key:数组元素 value:数组元素下标
for (int i = 0; i < nums.size(); i++) {
auto it = map.find(target - nums[i]);
if (it != map.end())
return {it->second, i};
map.insert({nums[i], i});
}
return {};
}
};
5. 四数相加II(unordered_map,分组 + 哈希)※
给定四个长度相同的整数数组 A、B、C、D,计算有多少个元组 (i, j, k, l) 满足 A[i] + B[j] + C[k] + D[l] = 0。(454. 四数相加 II)
算法思想:可以将四个数组分成两组,A 和 B 为一组,C 和 D 为另外一组。
使用二重循环遍历 A 和 B,得到所有 a + b 的值并存入一个 unordered_map 中,其中 key 为 a + b 的数值,value 为该个 a + b 的数值出现的次数。
同样使用二重循环遍历 C 和 D。当遍历到 c + d 时,如果键 − (c + d) 出现在 unordered_map 中,则找到了满足条件的一个或多个四元组,将其对应的 value 累加进计数器中。
最终即可得到满足 A[i] + B[j] + C[k] + D[l] = 0 的四元组数目,时间复杂度为 O(n2)。
class Solution {
public:
int fourSumCount(vector<int> &nums1, vector<int> &nums2, vector<int> &nums3, vector<int> &nums4) {
unordered_map<int, int> map; // key:a+b的值 value:a+b的值出现的次数
for (int a : nums1)
for (int b : nums2)
map[a + b]++;
int result = 0;
for (int c : nums3)
for (int d : nums4)
if (map.find(-c - d) != map.end())
result += map[-c - d];
return result;
}
};
6. 赎金信(数组)
给定两个由小写英文字母组成的字符串 ransomNote 和 magazine,判断 ransomNote 能不能由 magazine 里面的字符构成。magazine 中的每个字符只能在 ransomNote 中使用一次。(383. 赎金信)
算法思想:用一个数组记录 magazine 中各字符出现的次数。对 ransomNote 中的每个字符,将其对应在哈希表中的值减 1。若遍历结束后哈希表中出现负值,则 ransomNote 不能由 magazine 里的字符构成。
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
vector<int> record(26, 0); // 记录magazine中各字符出现的次数
for (char ch : magazine)
record[ch - 'a']++;
for (char ch : ransomNote)
if (--record[ch - 'a'] < 0)
return false;
return true;
}
};
7. 三数之和(排序 + 双指针)※
给定一个整数数组 nums,判断是否存在三元组 [nums[i], nums[j], nums[k]] (i≠j≠k) 使得 nums[i] + nums[j] + nums[k] = 0,并返回所有满足条件的不重复的三元组。(15. 三数之和)
分析:若本题使用哈希表法,则需使用一个二重循环遍历 nums[i] 和 nums[j],再使用哈希法确定第三个数 nums[k]。但是,由于这三个数出自同一个数组中,并且还需要去重,使用这种方法将十分棘手。
算法思想:本题采用双指针法更合适。
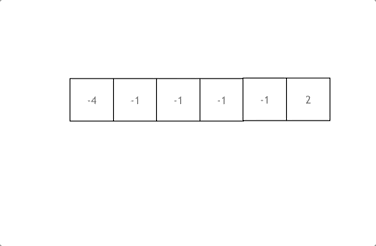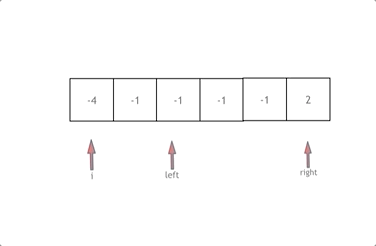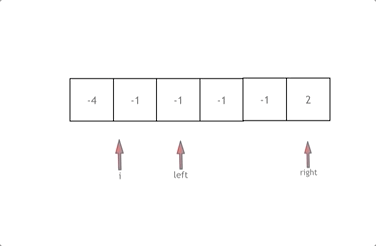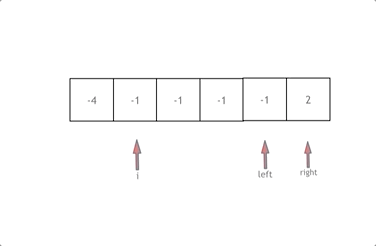
先将数组从小到大排序,使用一个工作指针 i 来确定三元组中的第一个元素。遍历时,要对 nums[i] 进行去重。对每个 i,定义两个指针 left 和 right 来确定三元组中的后两个元素,初始 left = i + 1,right = nums.size()-1。计算 nums[i] + nums[left] + nums[right] 的值,若小于 0 则 left 右移,若大于 0 则 right 左移,直到找到和为 0 的三元组。找到后,还需要对 nums[left] 和 nums[right] 进行去重,继续查找直到 left 与 right 相遇为止。总的时间复杂度为 O(n2)。
class Solution {
public:
vector<vector<int>> threeSum(vector<int> &nums) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > 0) // 排序后最小元素大于0, 一定不存在和为0的三元组(剪枝)
return result;
if (i > 0 && nums[i] == nums[i - 1]) // 对nums[i]去重
continue;
int left = i + 1, right = nums.size() - 1;
while (left < right) {
int sum = nums[i] + nums[left] + nums[right];
if (sum < 0)
left++;
else if (sum > 0)
right--;
else {
result.push_back({nums[i], nums[left], nums[right]});
// 找到一个三元组后, 对nums[left]和nums[right]去重
while (left < right && nums[left] == nums[left + 1])
left++;
while (left < right && nums[right - 1] == nums[right])
right--;
// 找到答案时, 双指针同时收缩
left++;
right--;
}
}
}
return result;
}
}
8. 四数之和(排序 + 双指针)
给定一个整数数组 nums 和目标值 target,返回所有满足 nums[a] + nums[b] + nums[c] + nums[d] = target 的不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (a≠b≠c≠d)。(18. 四数之和)
算法思想:在15. 三数之和的实现上再嵌套一层循环即可,时间复杂度为 O(n3)。
【注】本题与上题都可使用剪枝进行一定加速,注意两题中剪枝判断条件的不同。
class Solution {
public:
vector<vector<int>> fourSum(vector<int> &nums, int target) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
for (int a = 0; a < nums.size(); a++) {
if (nums[a] > target && nums[a] >= 0) // 剪枝
break;
if (a > 0 && nums[a] == nums[a - 1]) // 对nums[a]去重
continue;
for (int b = a + 1; b < nums.size(); b++) {
if (nums[a] + nums[b] > target && nums[a] + nums[b] >= 0) // 二级剪枝
break;
if (b > a + 1 && nums[b] == nums[b - 1]) // 对nums[b]去重
continue;
int c = b + 1, d = nums.size() - 1;
while (c < d) {
// 使用long类型(8位)防止溢出
long sum = (long)nums[a] + nums[b] + nums[c] + nums[d];
if (sum < target)
c++;
else if (sum > target)
d--;
else {
result.push_back({nums[a], nums[b], nums[c], nums[d]});
while (c < d && nums[c] == nums[c + 1]) // 对nums[c]去重
c++;
while (c < d && nums[d - 1] == nums[d]) // 对nums[d]去重
d--;
c++;
d--;
}
}
}
}
return result;
}
};
字符串
1. 反转字符串
原地反转字符数组。(344. 反转字符串)
class Solution {
public:
void reverseString(vector<char> &s) {
for (int i = 0; i < s.size() / 2; i++)
swap(s[i], s[s.size() - 1 - i]);
}
};
【注】<algorithm> 头文件提供了库函数
std::reverse,可用于 string、vector 等容器类型:reverse(s.begin(), s.end()); // 反转整个字符串 reverse(s.begin() + i, s.begin() + j); // 反转 s[i..j-1] (迭代器范围是左闭右开区间)
2. 反转字符串II
给定字符串 s 和整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
- 如果剩余字符少于 k 个,则将剩余字符全部反转。
- 如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。(541. 反转字符串 II)
class Solution {
public:
string reverseStr(string s, int k) {
for (int i = 0; i < s.size(); i += 2 * k)
if (s.size() - i < k) // 剩余字符少于k个
reverse(s.begin() + i, s.end());
else
reverse(s.begin() + i, s.begin() + i + k); // 反转s[i..i+k-1]
return s;
}
};
3. 替换数字(数组扩容 + 双指针)
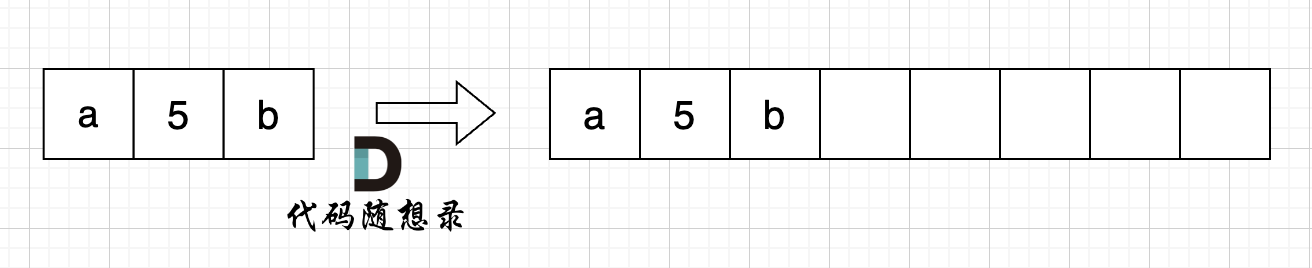
给定一个包含小写字母和数字字符的字符串 s,将 s 中的字母字符保持不变,而将每个数字字符替换为 “number”。 (54. 替换数字 - 卡码网KamaCoder)
解法一:首先将字符数组扩容到替换后的大小,再令指针 i 和 j 分别指向新长度和旧长度的末尾,从后向前替换。
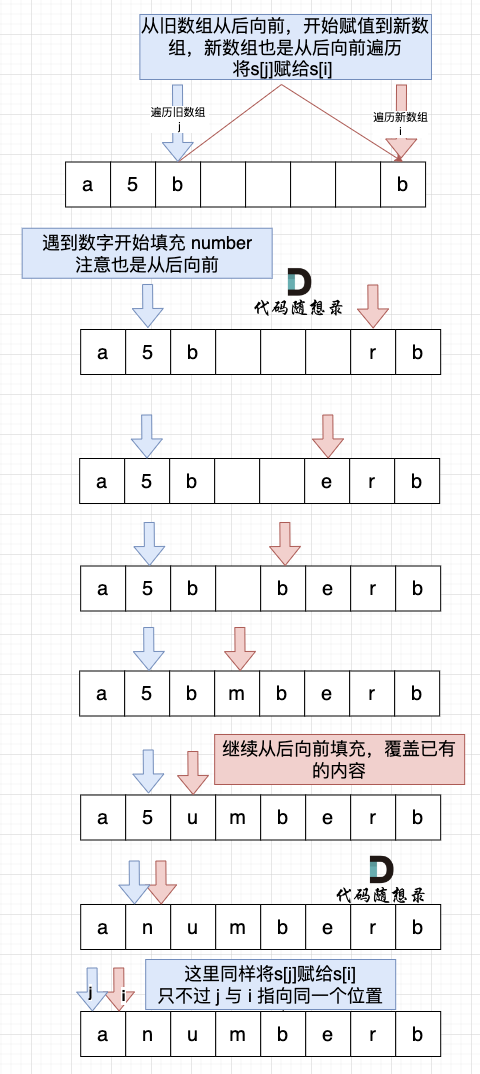
class Solution {
public:
string replaceDigits(string s) {
int i = s.size() - 1, count = 0; // 统计数字字符个数
for (char ch : s)
if (ch >= '0' && ch <= '9')
count++;
s.resize(s.size() + count * 5); // 数组扩容
int j = s.size() - 1;
for (; i >= 0; i--)
if (s[i] >= 'a' && s[i] <= 'z')
s[j--] = s[i];
else {
s[j--] = 'r';
s[j--] = 'e';
s[j--] = 'b';
s[j--] = 'm';
s[j--] = 'u';
s[j--] = 'n';
}
return s;
}
};
解法二:使用库函数replace()。
class Solution {
public:
string replaceDigits(string s) {
for (int i = 0; i < s.size(); i++)
if (s[i] >= '0' && s[i] <= '9')
s.replace(i, 1, "number"); // 从位置i开始,替换1个字符为"number"
return s;
}
};
4. 反转字符串中的单词(双指针)※
反转字符串中单词的顺序。输入字符串中可能会存在前导空格、尾随空格或者单词间的多个空格。反转后的字符串中,单词间应当仅用单个空格分隔,且不能包含前导空格和尾随空格。要求空间复杂度为 O(1)。(151. 反转字符串中的单词)
输入:" the sky is blue "
输出:"blue is sky the"
算法思想:
去除冗余空格 →
"the sky is blue"将整个字符串反转 →
"eulb si yks eht"将每个单词反转 →
"blue is sky the"
其中第一步操作可以借用27. 移除元素中的思想,用 k 记录 s 中应保留字符的个数,将应保留的字符移动至下标 k 的位置。在移除空格时要在相邻单词之间保留一个空格,最后调整字符串的长度。
class Solution {
public:
string reverseWords(string s) {
int k = 0; // 用k记录s中应保留字符的个数
for (int i = 0; i < s.size(); i++) // 去除冗余空格
if (s[i] != ' ') {
if (k != 0)
s[k++] = ' '; // 对于非首词前面留一空格
while (i < s.size() && s[i] != ' ')
s[k++] = s[i++]; // 将应保留的字符移动至下标k的位置
}
s.resize(k); // 调整字符串长度
reverse(s.begin(), s.end()); // 反转字符串
for (int i = 0, start = 0; i <= s.size(); i++)
if (i == s.size() || s[i] == ' ') {
reverse(s.begin() + start, s.begin() + i); // 反转每个单词
start = i + 1;
}
return s;
}
};
5. 右旋字符串
将字符串 s 的后 k 个字符移到字符串的前面。 (55. 右旋字符串 - 卡码网KamaCoder)
输入:s = "abcdefg", k = 2
输出:"fgabcde"
算法思想:三次reverse。
class Solution {
public:
string rightRotate(string s, int k) {
reverse(s.begin(), s.end()); // 反转 s[0..n-1]
reverse(s.begin(), s.begin() + k); // 反转 s[0..k-1]
reverse(s.begin() + k, s.end()); // 反转 s[k..n-1]
return s;
}
};
6. 实现 strStr() (KMP算法)※
返回模式串 t 在主串 s 中第一个匹配项的下标(下标从 0 开始)。如果失配,则返回 -1 。(28. 找出字符串中第一个匹配项的下标)
算法思想:KMP算法原题。
一、next 数组实现:记模式串为 \(\text{“}p_{0}\cdots p_{n}\text{”}\) ,则 \(\mathrm{next}[i]\) 表示 \(\text{“}p_{0}\cdots p_{i-1}\text{”}\) 的最长公共前后缀长度。具体而言,
\[\mathrm{next}[i]= \begin{cases} -1,&i=0\\ \max\{j|0<j<i\text{ 且 “}p_0\cdots p_{j-1}\text{”}=\text{“}p_{i-j}\cdots p_{i-1}\text{”}\},&\text{当此集合不空时}\\ 0,&\text{其他情况} \end{cases}\]KMP 算法中,当子串的第 \(i\) 个字符与主串发生失配时,跳到子串的 \(\mathrm{next}[i]\) 位置重新与主串当前位置进行比较。next 数组可以通过递推计算。首先,\(\mathrm{next}[0] = -1\)。设 \(\mathrm{next}[i]=j\),即 \(\text{“}p_0\cdots p_{j-1}\text{”}=\text{“}p_{i-j}\cdots p_{i-1}\text{”}\),分两种情况讨论:
- \(p_j=p_i\),此时有 \(\text{“}p_0\cdots p_{j-1}p_{j}\text{”}=\text{“}p_{i-j}\cdots p_{i-1}p_{i}\text{”}\),即 \(\mathrm{next}[i+1]=j+1=\mathrm{next}[i]+1\)。
- \(p_j\neq p_i\),此时需重新寻找 \(\text{“}p_{0}\cdots p_{i}\text{”}\) 的最长公共前后缀长度,可将其视为一个模式匹配的问题。用前缀 \(\text{“}p_0\cdots p_{j}\text{”}\) 去与后缀 \(\text{“}p_{i-j}\cdots p_{i}\text{”}\) 匹配,当 \(p_j\neq p_i\) 时,应将 \(\text{“}p_0\cdots p_{j}\text{”}\) 向右滑动至以第 \(\mathrm{next}[j]\) 个字符与 \(p_i\) 比较,若 \(p_{\mathrm{next}[j]}\) 与 \(p_i\) 仍不匹配,则需要寻找长度更短的公共前后缀,下一步继续用 \(p_{\mathrm{next}[\mathrm{next}[j]]}\) 与 \(p_i\) 比较,以此类推,直到找到某个更小的 \(j'=\mathrm{next}[\mathrm{next}\cdots[j]]\,(0<j^\prime<j<i)\) 满足 \(\text{“}p_0\cdots p_{j^\prime}\text{”}=\text{“}p_{i-j^\prime}\cdots p_{i}\text{”}\),则 \(\mathrm{next}[i+1]=j'+1\)。也可能不存在任何 \(j^\prime\)满足上述条件,即不存在长度更短的公共前后缀,此时有 \(\mathrm{next}[i+1]=0\)。
class Solution {
public:
int strStr(string s, string t) {
// 1.计算next数组
vector<int> next(t.size(), -1);
for (int i = 0, j = -1; i < t.size() - 1;) {
if (j == -1 || t[i] == t[j])
next[++i] = ++j; // 若t[i]==t[j],则next[j+1]=next[j]+1
else
j = next[j]; // 否则令j=next[j],循环继续
}
// 2.使用KMP算法匹配
for (int i = 0, j = 0; i < s.size();) {
if (j == -1 || s[i] == t[j]) {
i++;
j++;
if (j == t.size())
return i - t.size(); // 匹配成功
} else
j = next[j]; // 模式串向右滑动
}
return -1;
}
};
二、nextval 数组实现:对 next 数组进行改进,若出现 \(p_j=p_{\mathrm{next}[j]}\),则需要再次递归,将 \(\mathrm{next}[j]\) 修正为 \(\mathrm{next}[\mathrm{next}[j]]\),直至两者不相等为止。新数组即为 nextval,此时匹配算法不变。
class Solution {
public:
int strStr(string s, string t) {
// 1.计算nextval数组
vector<int> nextval(t.size(), -1);
for (int i = 0, j = -1; i < t.size() - 1;) {
if (j == -1 || t[i] == t[j]) {
if (t[++i] == t[++j])
nextval[i] = nextval[j];
else
nextval[i] = j;
} else
j = nextval[j];
}
// 2.使用KMP算法匹配
for (int i = 0, j = 0; i < s.size();) {
if (j == -1 || s[i] == t[j]) {
i++;
j++;
if (j == t.size())
return i - t.size(); // 匹配成功
} else
j = nextval[j]; // 模式串向右滑动
}
return -1;
}
};
【注】在 C 语言中,<string.h> 的库函数
char *strstr(const char *s, const char *t)返回子串 t 在 主串 s 中第一次出现的位置(指向该位置的指针),若未找到则返回 NULL。在 C++ 中,std::string 的成员函数 find() 的作用与 strstr() 类似,调用
s.find(t)直接返回子串 t 在主串 s 中位置的下标。若未找到,返回一个特殊标记string::npos(其值等于 size_t 类型能表示的最大值)。
7. 重复的子字符串(移动匹配、KMP算法)※
检查一个非空字符串 s 是否可以由它的一个子串重复多次构成。(459. 重复的子字符串)
解法一:将两个 s 拼接在一起,若中间还出现一个 s(去除首尾字符)\(\iff\) s 由重复子串组成。[证明]
class Solution {
public:
bool repeatedSubstringPattern(string s) {
string t = s + s;
t.erase(t.begin());
t.erase(t.end() - 1); // 去除首尾字符
return t.find(s) != string::npos; // 找到则返回true
}
};
解法二( next 数组):s 的最长公共前后缀不包含的那部分子串是 s 的最小重复子串 \(\iff\) s 由重复子串组成。
而如果 s 的最长公共前后缀不包含的子串的长度可以被 s 的长度整除,那么这部分子串就是 s 的最小重复子串。
例如,对于字符串 “abcdabcdabcd”,为计算其最长公共前后缀,可以添加一个任意字符后再计算 next 数组:
| a | b | c | d | a | b | c | d | a | b | c | d | * | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| next[] | -1 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
可知最长公共前后缀(即 “abcdabcd”)的长度为 8,它所不包含的子串 “abcd” 的长度为 12 - 8 = 4。由于 12 mod 4 = 0,故子串 “abcd” 就是 s 的最小重复子串。[证明]
class Solution {
public:
bool repeatedSubstringPattern(string s) {
// 1.计算next数组
string t = s + '*'; // 添加一个任意字符
vector<int> next(t.size(), -1);
for (int i = 0, j = -1; i < t.size() - 1;) {
if (j == -1 || t[i] == t[j])
next[++i] = ++j;
else
j = next[j];
}
// 2. 求最小重复子串
int len = next[s.size()]; // 最长公共前后缀的长度
return len != 0 && s.size() % (s.size() - len) == 0;
}
};
栈与队列
在 STL 中,栈和队列被归类为容器适配器,可以由 vector、deque、list 等容器作为底层实现,默认使用 deque 作为底层容器,也可以人为指定其使用的底层容器。
stack<int> s; queue<int> q; // 默认使用 deque 作为底层容器 stack<int, vector<int>> s; // 指定使用 vector 作为底层容器的栈 queue<int, list<int>> q; // 指定使用 list 作为底层容器的队列
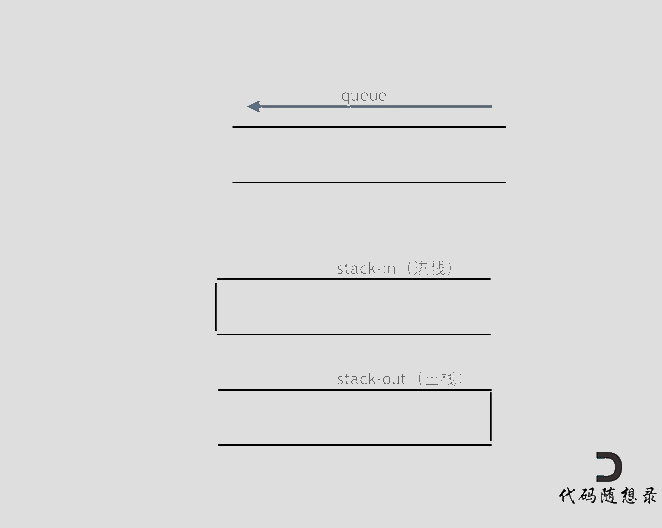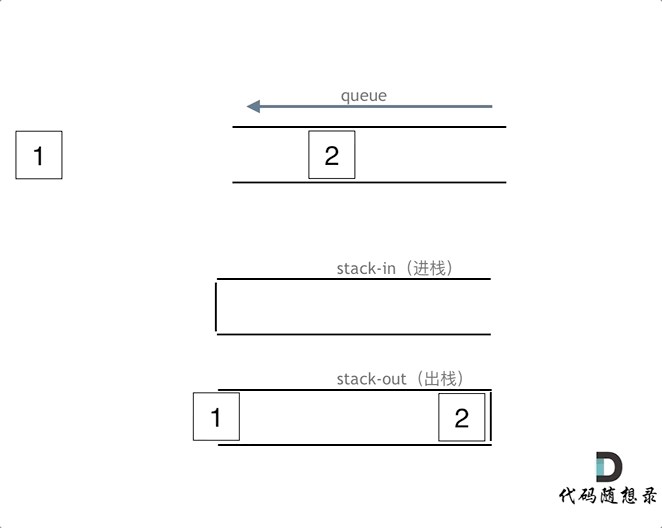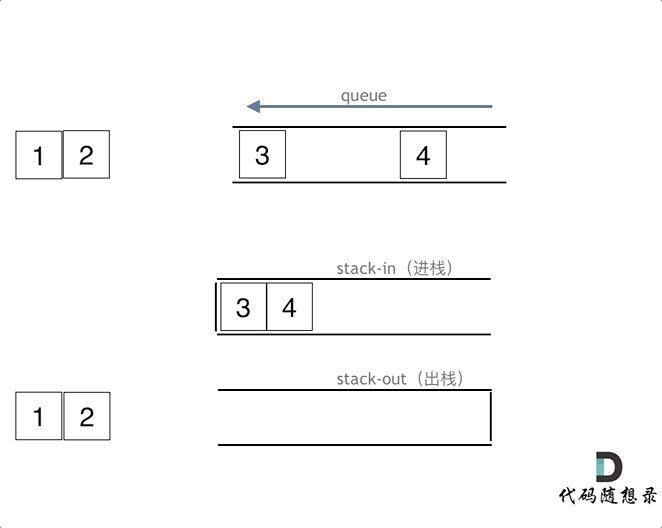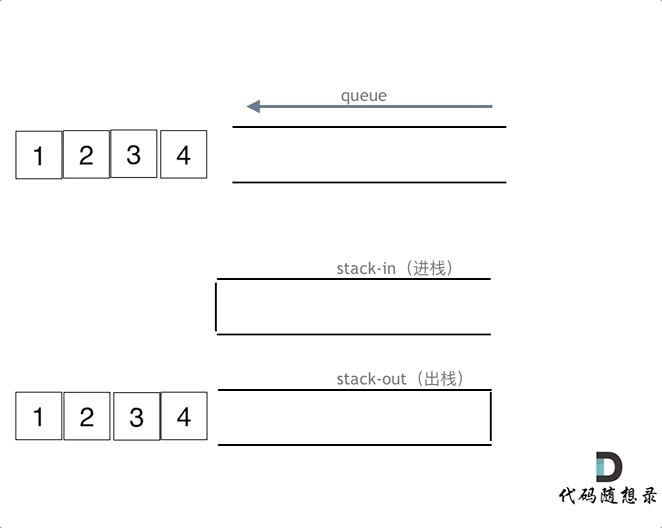
1. 用栈实现队列
算法思想:使用一个输入栈和一个输出栈。(232. 用栈实现队列)
- 入队时,将元素放入输入栈中即可。
- 出队时,若输出栈为空,则先将输入栈中的所有元素全部出栈并入栈到输出栈中,再从输出栈中弹出元素;否则直接从输出栈中弹出元素即可。
- 当输入栈和输出栈都为空时,队列为空。
该实现 push()、pop()、front() 操作的时间复杂度均为 O(1)。
class MyQueue {
public:
MyQueue() {}
void push(int x) { // 队尾插入
sIn.push(x);
}
int pop() { // 队头删除
if (sOut.empty())
while (!sIn.empty()) { // 先将输入栈中的所有元素移入输出栈中
sOut.push(sIn.top());
sIn.pop();
}
int x = sOut.top();
sOut.pop();
return x;
}
int peek() { // 返回队头元素
if (sOut.empty())
while (!sIn.empty()) {
sOut.push(sIn.top());
sIn.pop();
}
return sOut.top();
}
bool empty() { // 判空
return sIn.empty() && sOut.empty();
}
private:
stack<int> sIn, sOut; // 输入栈和输出栈
};
2. 用队列实现栈 ※
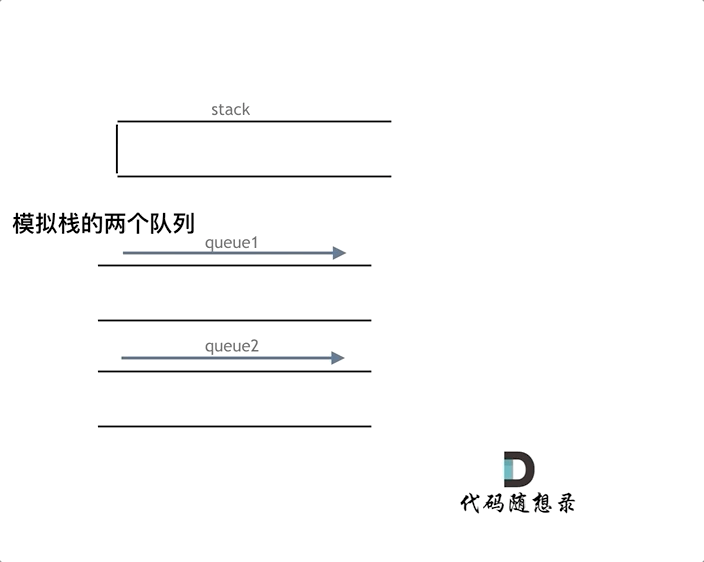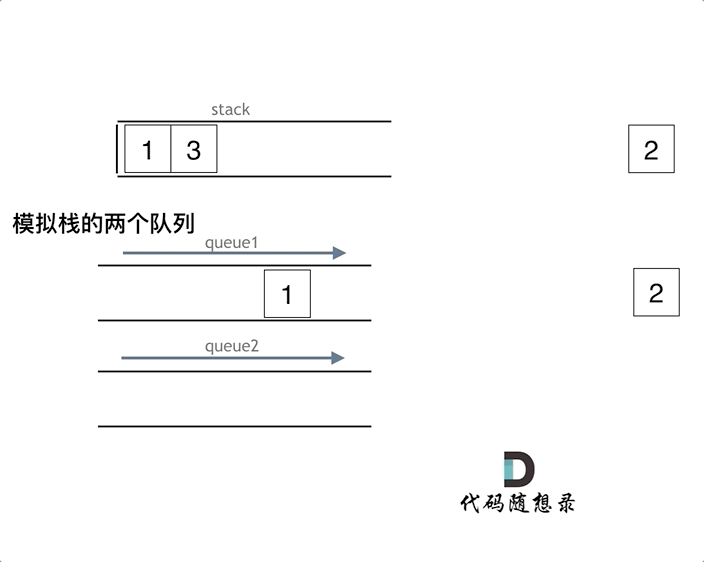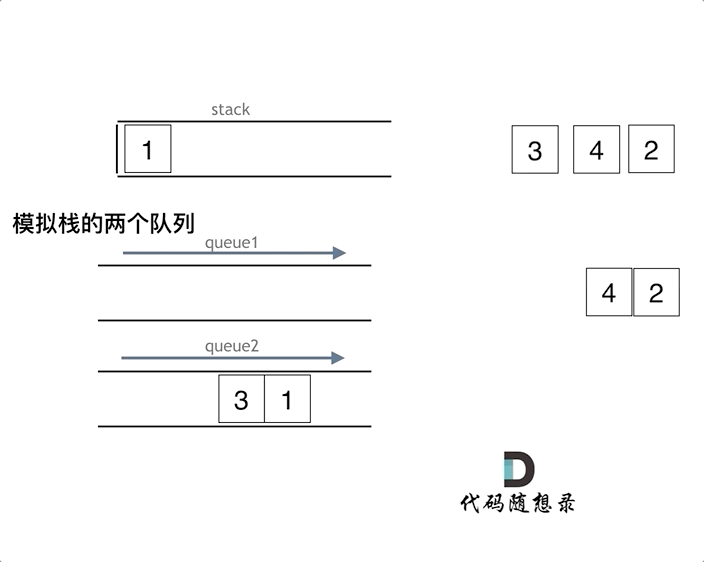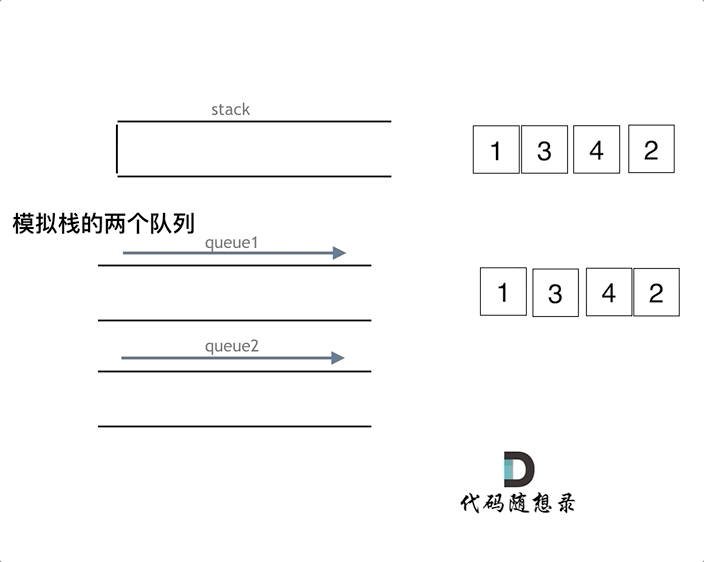
解法一:使用两个队列。(225. 用队列实现栈)
- 队列 q1 用来进行插入和删除操作,q1 为空时栈为空。
- 队列 q2 用来在进行删除操作时为 q1进行备份,即当要弹出栈顶元素(即 q1 的队尾元素)时,将栈顶以下的元素(即 q1 队尾之前的元素)从 q1 暂存入 q2,弹出操作完成后再将这些元素移回 q1。
该实现 push() 操作的时间复杂度为 O(1),pop() 和 top() 操作的时间复杂度为 O(n)。
class MyStack {
public:
MyStack() {}
void push(int x) { // 入栈
q1.push(x);
}
int pop() { // 出栈
while (q1.size() > 1) {
q2.push(q1.front());
q1.pop();
}
int x = q1.front();
q1.pop();
while (!q2.empty()) {
q1.push(q2.front());
q2.pop();
}
return x;
}
int top() { // 获取栈顶元素(实际上就是q1.back())
while (q1.size() > 1) {
q2.push(q1.front());
q1.pop();
}
int x = q1.front();
q2.push(q1.front());
q1.pop();
while (!q2.empty()) {
q1.push(q2.front());
q2.pop();
}
return x;
}
bool empty() { // 判空
return q1.empty();
}
private:
queue<int> q1, q2;
};
解法二:只使用一个队列。实际上,为了进行删除操作将队尾之前的元素用一个额外的队列暂存是多余的。删除时,只需要将队尾之前的元素依次出队再重新添加至队尾,此时待删除元素便移动到了队头,删除即可。
class MyStack {
public:
MyStack() {}
void push(int x) { // 入栈
q.push(x);
}
int pop() { // 出栈
int size = q.size();
while (--size) {
q.push(q.front());
q.pop();
}
int x = q.front();
q.pop();
return x;
}
int top() { // 获取栈顶元素
int size = q.size();
while (--size) {
q.push(q.front());
q.pop();
}
int x = q.front();
q.push(q.front());
q.pop();
return x;
}
bool empty() { // 判空
return q.empty();
}
private:
queue<int> q;
};
3. 有效的括号(栈)
给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。(20. 有效的括号)
算法思想:括号匹配问题。
- 初始设置一个空栈,顺序读入括号。
- 若为左括号,入栈。
- 若为右括号,检查它是否与栈顶的左括号匹配。若匹配,则将栈顶出栈,继续读入;否则,字符串无效。
class Solution {
public:
bool isValid(string s) {
stack<char> stk;
unordered_map<char, char> map = {{')', '('}, {']', '['}, {'}', '{'}};
for (char ch : s) {
if (map.find(ch) == map.end()) // ch为左括号,入栈
stk.push(ch);
else if (!stk.empty() && map[ch] == stk.top()) // ch为右括号且与栈顶匹配,栈顶出栈
stk.pop();
else
return false;
}
return stk.empty();
}
};
4. 删除字符串中的所有相邻重复项(栈)
反复选择字符串中两个相邻且相同的字母并删除,直到无法继续删除。(1047. 删除字符串中的所有相邻重复项)
算法思想:与括号匹配类似。遍历字符串,用栈存放遍历过的元素,若当前元素与栈顶元素相同,将栈顶元素弹出。遍历完成后,栈中的剩余元素即为最终结果。
class Solution {
public:
string removeDuplicates(string s) {
stack<char> stk;
for (char ch : s) {
if (!stk.empty() && stk.top() == ch)
stk.pop();
else
stk.push(ch);
}
string result;
while (!stk.empty()) {
result = stk.top() + result;
stk.pop();
}
return result;
}
};
【注】
std::string类提供了 empty()、back()、push_back()、pop_back() 等成员函数,因此可以直接用字符串模拟栈,省去了将栈再转为字符串的步骤。class Solution { public: string removeDuplicates(string s) { string result; for (char ch : s) { if (!result.empty() && result.back() == ch) result.pop_back(); else result.push_back(ch); } return result; } };
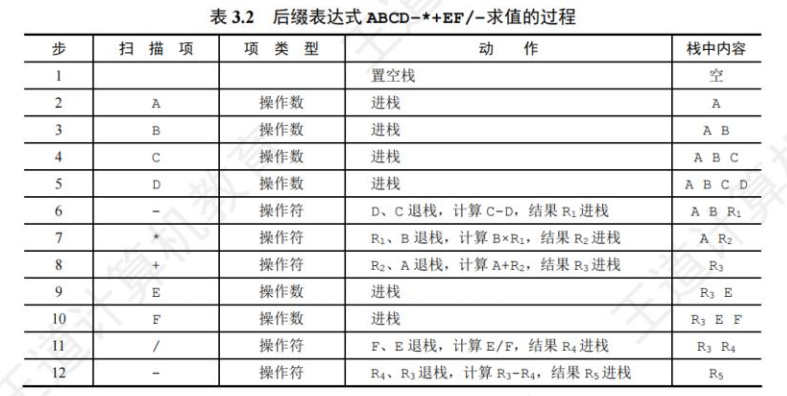
5. 逆波兰表达式求值(栈)
计算后缀表达式的值。(150. 逆波兰表达式求值)
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:对应的中缀表达式为:((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = 22
算法思想:从左往右依次扫描表达式的每一项,若该项是操作数, 则将其入栈;若该项是操作符 <op>,则从栈中退出两个操作数 Y 和 X,形成运算指令 X<op>Y,并将计算结果压入栈中。当所有项都扫描并处理完后,栈顶存放的就是最后的计算结果。
class Solution {
public:
int evalRPN(vector<string> &tokens) {
stack<int> s; // 存放操作数
for (string op : tokens) {
if (op == "+" || op == "-" || op == "*" || op == "/") {
int y = s.top();
s.pop();
int x = s.top();
s.pop();
if (op == "+")
s.push(x + y);
if (op == "-")
s.push(x - y);
if (op == "*")
s.push(x * y);
if (op == "/")
s.push(x / y);
} else
s.push(stoi(op)); // string转int
}
return s.top();
}
};
【注】<string> 中的
stoi()函数可将 string 类型字符串转化为 int 型整数(C++11)。常用的还有stoll()(long long)、stod()(double) 等。
6. 滑动窗口最大值(单调队列)※
一个大小为 k 的滑动窗口在数组 nums 上从左向右逐位移动,返回滑动窗口中的最大值。(239. 滑动窗口最大值)
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
算法思想:我们希望实现一个队列,可以实时获取到队列中元素的最大值。这可以借助单调队列来实现。
【注】维护元素单调递减或递增的队列就叫作单调队列。本题中定义的单调队列里的 push 和 pop 接口仅适用于本题,单调队列的实现不是一成不变的,在不同问题场景下会有不同的写法。
解法一:自行实现单调队列类。(时间复杂度为 O(n))
本题所采用的单调队列是一个这样的队列:单调队列中的元素从滑动窗口中选取,要求队列中的元素从大到小排列,且元素的先后顺序与滑动窗口中的顺序相同。
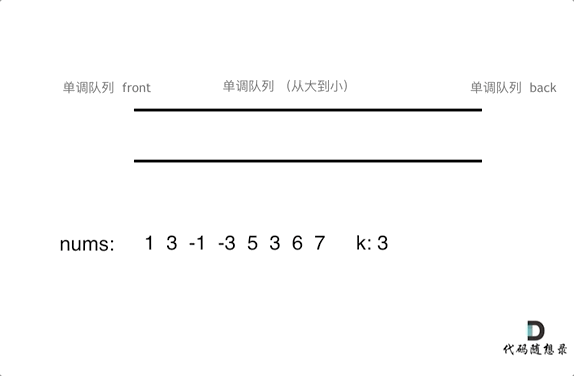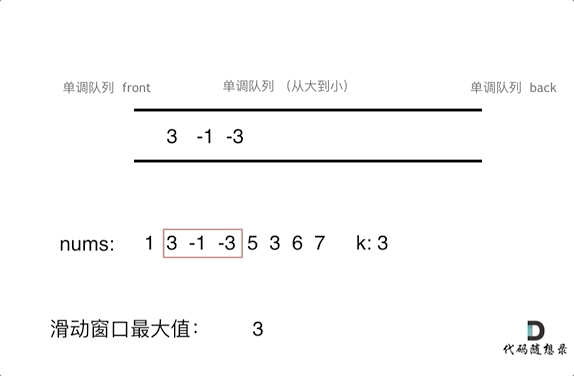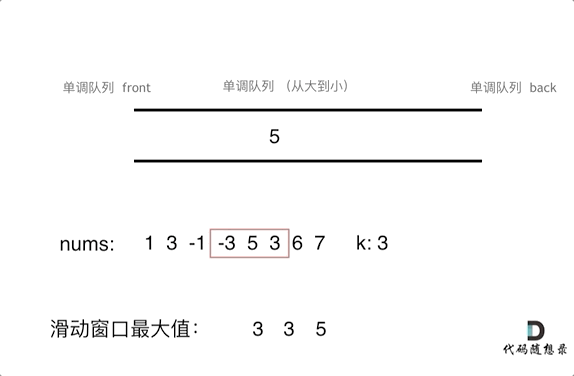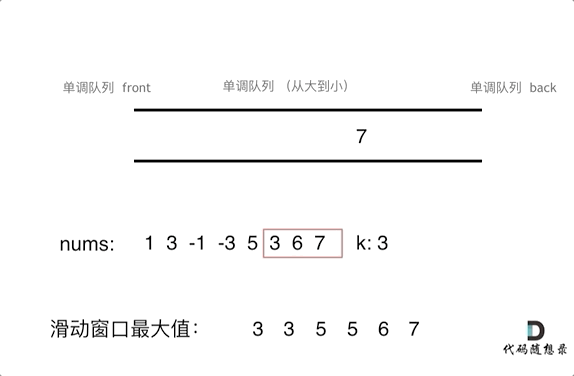
因此,单调队列的队头 front() 总是存放窗口中的最大元素。定义单调队列的 push() 和 pop() 操作如下:
当新元素 value 进入窗口时,执行 push(value):若有小于 value 的值,则将它们全部从队尾弹出,再将 value 插入队尾,保证没有比 value 更小的元素。
当旧元素 value 移出窗口时,执行 pop(value):若该元素是原窗口中的最大元素,它此时位于单调队列的队头,直接出队即可;否则,该元素一定不在单调队列中(因为窗口中在它之后有更大的元素),不执行任何操作。
可见,用双端队列 deque 容器实现单调队列比较合适。
class MyQueue { // 单调队列类
public:
void push(int value) {
while (!q.empty() && q.back() < value)
q.pop_back();
q.push_back(value);
}
void pop(int value) {
if (!q.empty() && q.front() == value)
q.pop_front();
}
int front() {
return q.front();
}
private:
deque<int> q;
};
class Solution {
public:
vector<int> maxSlidingWindow(vector<int> &nums, int k) {
MyQueue q;
vector<int> result;
for (int i = 0; i < k; i++)
q.push(nums[i]);
result.push_back(q.front());
for (int i = k; i < nums.size(); i++) {
q.pop(nums[i - k]);
q.push(nums[i]);
result.push_back(q.front());
}
return result;
}
};
解法二:使用 multiset 实现单调队列的功能。(时间复杂度不如解法一)
multiset 是有序可重复的集合,默认升序。窗口滑动时,将新元素加入集合和把旧元素从集合中删除可以用insert()和erase()函数实现。rbegin()函数返回指向 multiset 容器最后一个元素的反向迭代器,因此*s.rbegin()可以直接获取集合中的最大值。
class Solution {
public:
vector<int> maxSlidingWindow(vector<int> &nums, int k) {
multiset<int> s;
vector<int> result;
for (int i = 0; i < k; i++)
s.insert(nums[i]);
result.push_back(*s.rbegin());
for (int i = k; i < nums.size(); i++) {
s.erase(s.find(nums[i - k])); // 若直接用s.erase(nums[i-k])会删除所有值为nums[i-k]的元素
s.insert(nums[i]);
result.push_back(*s.rbegin());
}
return result;
}
};
7. 前 K 个高频元素(优先队列)※
返回整数数组 nums 中出现频率前 k 高的元素,可以按任意顺序返回答案。(347. 前 K 个高频元素)
算法思想:可以用一个 unordered_map 统计各元素的频率,这就转化为找最大 k 个数的 TopK 问题。一般的方法是,使用一个大小为 k 的数组,读入前 k 个数建立小根堆,之后依次读入剩下的数,若小于堆顶则舍弃,否则用该数取代堆顶并重新调整堆,最后堆中的数即为所求。
C++ 提供了优先队列 priority_queue 这一容器适配器,它允许我们快速访问队列中具有最高(或最低)优先级的元素,默认是一个大根堆。声明一个自定义类型的优先队列时,需要提供比较函数。小根堆即可通过自定义比较函数来实现。通过使用 priority_queue,向堆中添加元素和删除堆顶元素都可分别用 push() 和 pop() 接口简明实现。
class Compare {
public:
bool operator()(const pair<int, int> &a, const pair<int, int> &b) { // 比较函数
return a.second > b.second; // 小根堆
}
};
class Solution {
public:
vector<int> topKFrequent(vector<int> &nums, int k) {
unordered_map<int, int> map;
for (int num : nums)
map[num]++; // 统计各元素频率
priority_queue<pair<int, int>, vector<pair<int, int>>, Compare> q;
for (const auto &pair : map) {
if (q.size() < k)
q.push(pair); // 前k个直接入堆
else if (pair.second > q.top().second) {
q.pop();
q.push(pair);
}
}
vector<int> result;
while (!q.empty()) {
result.push_back(q.top().first);
q.pop();
}
reverse(result.begin(), result.end()); // 此时result按频率从小到大排列,需进行逆置
return result;
}
};
【注】小根堆的比较函数可以通过使用重载运算符的函数对象实现:
class Compare { public: bool operator()(int a, int b) { // 函数对象是一个重载了operator()的类的实例 return a > b; } }; priority_queue<int, vector<int>, Compare> q; // 存储元素的底层容器是vector也可以使用使用标准库函数对象
std:greater实现:priority_queue<int, vector<int>, greater<int>> q; // greater表示从小到大排列与之相对应的是标准库函数对象
std:less,故大根堆也可以写作:priority_queue<int, vector<int>, less<int>> q; // less表示从大到小排列
二叉树
LeetCode 对二叉树的定义:
struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode() : val(0), left(nullptr), right(nullptr) {} TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} };
1. 二叉树的递归遍历
先序遍历(144. 二叉树的前序遍历)
class Solution { public: void preorder(TreeNode *root, vector<int> &result) { if (root != nullptr) { result.push_back(root->val); preorder(root->left, result); preorder(root->right, result); } } vector<int> preorderTraversal(TreeNode *root) { vector<int> result; preorder(root, result); return result; } };中序遍历(94. 二叉树的中序遍历)
class Solution { public: void inorder(TreeNode *root, vector<int> &result) { if (root != nullptr) { inorder(root->left, result); result.push_back(root->val); inorder(root->right, result); } } vector<int> inorderTraversal(TreeNode *root) { vector<int> result; inorder(root, result); return result; } };后序遍历(145. 二叉树的后序遍历)
class Solution { public: void postorder(TreeNode *root, vector<int> &result) { if (root != nullptr) { postorder(root->left, result); postorder(root->right, result); result.push_back(root->val); } } vector<int> postorderTraversal(TreeNode *root) { vector<int> result; postorder(root, result); return result; } };
2. 二叉树的迭代遍历 ※
先序遍历
解法一:
① 沿着根的左孩子,先访问结点,再入栈,直到左孩子为空。
② 栈顶元素出栈:若其右孩子为空,继续执行②;若其右孩子不空,将右子树转执行①。
class Solution { public: vector<int> preorderTraversal(TreeNode *root) { stack<TreeNode *> s; vector<int> result; TreeNode *p = root; while (p != nullptr || !s.empty()) { if (p != nullptr) { result.push_back(p->val); // 先访问结点再入栈 s.push(p); p = p->left; // 若左孩子不空,一路向左入栈 } else { p = s.top(); // 栈顶结点出栈 s.pop(); p = p->right; // 若其右孩子不空,向右子树走 } } return result; } };解法二:
① 根结点入栈。
② 栈顶元素出栈并访问:先将右孩子入栈,再将左孩子入栈(若有)。重复该步骤直到栈为空。

class Solution {
public:
vector<int> preorderTraversal(TreeNode *root) {
stack<TreeNode *> s;
vector<int> result;
if (root != nullptr)
s.push(root);
while (!s.empty()) {
TreeNode *p = s.top();
s.pop();
result.push_back(p->val); // 弹出栈顶元素并访问
if (p->right)
s.push(p->right); // 右孩子入栈
if (p->left)
s.push(p->left); // 左孩子入栈
}
return result;
}
};
中序遍历
① 沿着根的左孩子依次入栈,直到左孩子为空。
② 栈顶元素出栈并访问:若其右孩子为空,继续执行②;若其右孩子不空,将右子树转执行①。
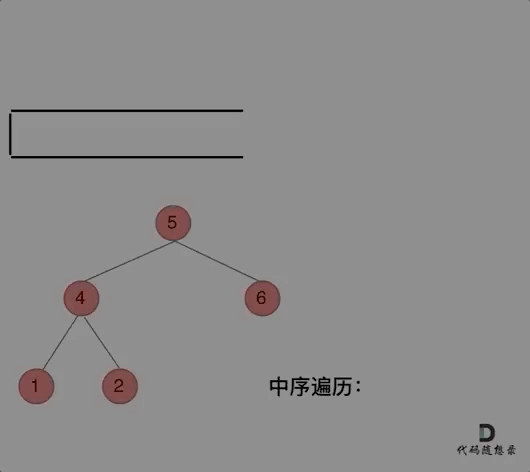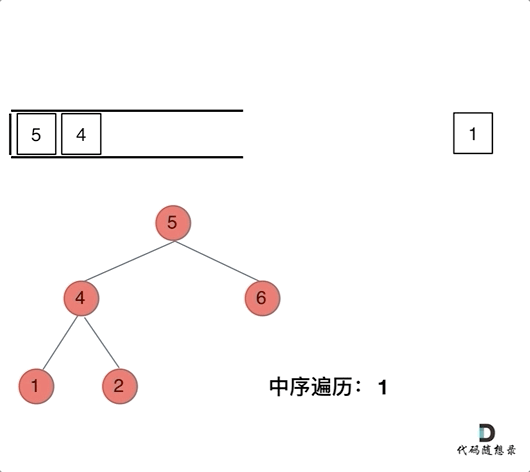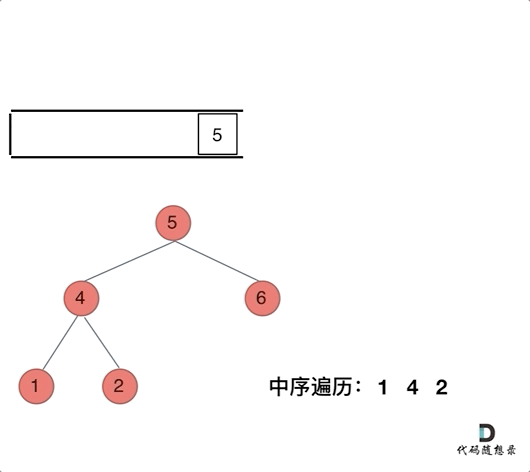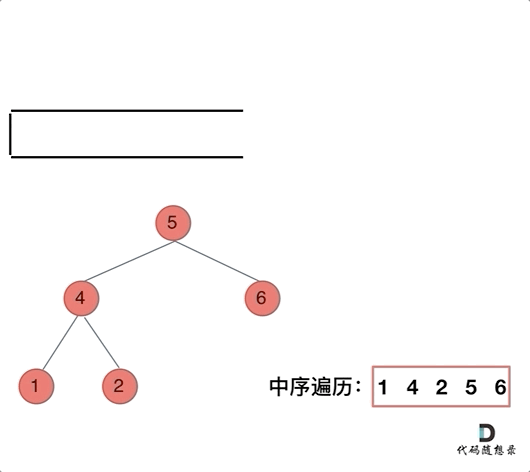
与前序遍历的解法一相比,只有访问结点操作和入栈操作的先后顺序不同。前序遍历先访问再入栈,中序遍历先入栈再访问。
class Solution {
public:
vector<int> inorderTraversal(TreeNode *root) {
stack<TreeNode *> s;
vector<int> result;
TreeNode *p = root;
while (p != nullptr || !s.empty()) {
if (p != nullptr) {
s.push(p);
p = p->left; // 若左孩子不空,一路向左入栈
} else {
p = s.top(); // 栈顶结点出栈并访问
s.pop();
result.push_back(p->val);
p = p->right; // 若其右孩子不空,向右子树走
}
}
return result;
}
};
后序遍历
① 根结点入栈。
② 栈顶元素出栈并访问:先将左孩子入栈,再将右孩子入栈(若有)。重复该步骤直到栈为空。
③ 将结果数组反转,便得到正确的后序序列。
与前序遍历的解法二相比,后序遍历除了要将结果数组反转,只有左右孩子入栈的顺序不同。先序遍历先将右孩子入栈,再将左孩子入栈;后序遍历先将左孩子入栈,再将右孩子入栈。
【注意】这种方法只适用于求取后序序列,遍历结点的顺序与后序序列正好相反。
class Solution { public: vector<int> postorderTraversal(TreeNode *root) { stack<TreeNode *> s; vector<int> result; if (root != nullptr) s.push(root); while (!s.empty()) { TreeNode *p = s.top(); s.pop(); result.push_back(p->val); // 弹出栈顶元素并访问 if (p->left) s.push(p->left); // 左孩子入栈 if (p->right) s.push(p->right); // 右孩子入栈 } reverse(result.begin(), result.end()); // 反转结果数组 return result; } };
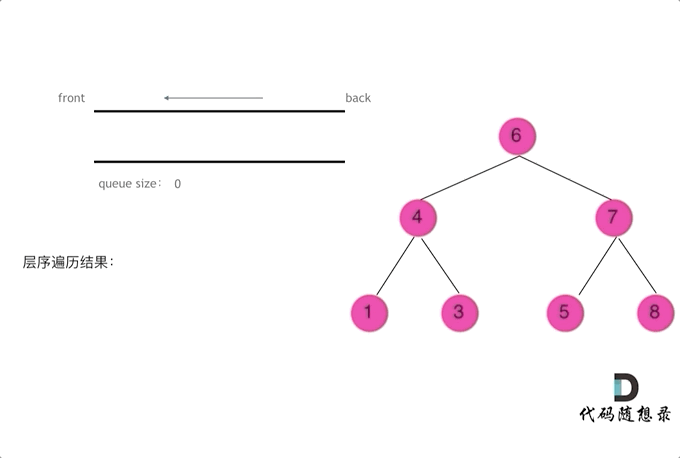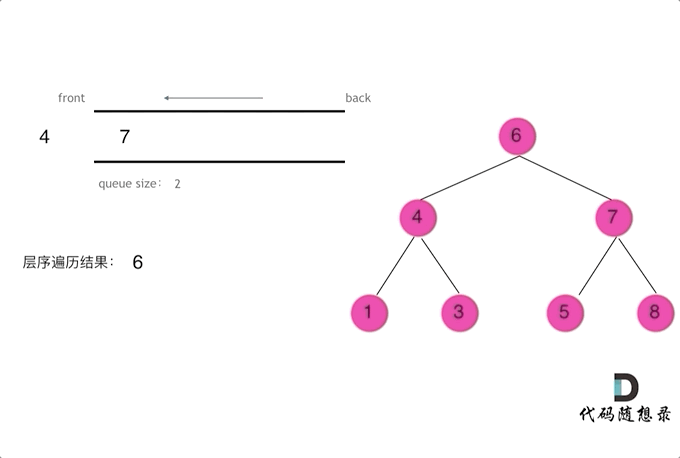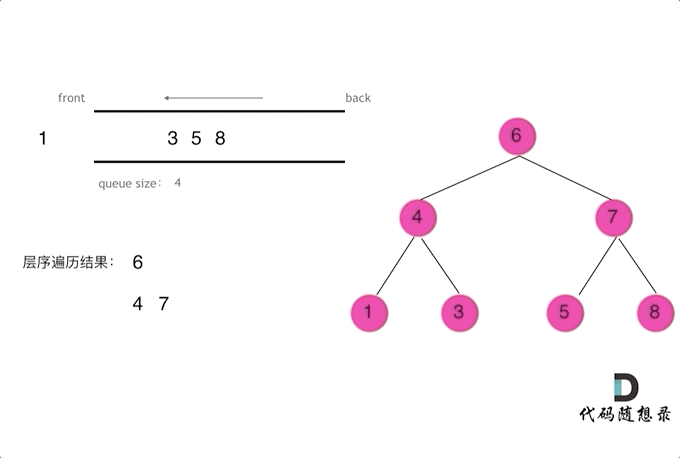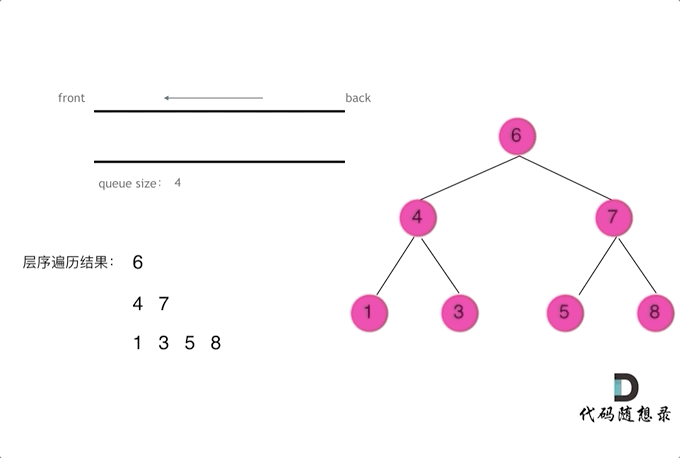
3. 二叉树的层序遍历 ※
① 根结点入队。
② 若队列非空,队头结点出队并访问,将其左右孩子入队(若有)。重复该步骤直到队列为空。
在每层迭代开始前,用 size 记录队列中当前的元素个数,以统计本层的结点数量,从而达到分层的目的。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode *root) {
queue<TreeNode *> q;
vector<vector<int>> result;
if (root != nullptr)
q.push(root);
while (!q.empty()) {
int size = q.size(); // 统计当前层的结点数量
vector<int> vec; // 记录每一层的结点
while (size--) {
TreeNode *p = q.front();
q.pop();
vec.push_back(p->val); // 队头结点出队并访问
if (p->left)
q.push(p->left);
if (p->right)
q.push(p->right); // 左右孩子入队
}
result.push_back(vec);
}
return result;
}
};
4. 翻转二叉树
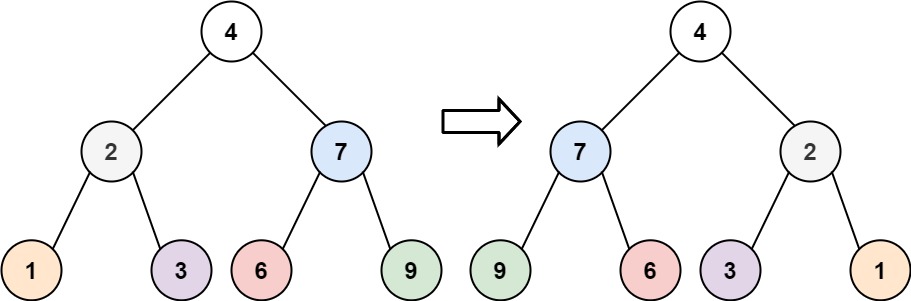
解法一:递归
class Solution {
public:
TreeNode *invertTree(TreeNode *root) {
if (root != nullptr) {
TreeNode *left = invertTree(root->right); // 翻转后的右子树作为新的左子树
TreeNode *right = invertTree(root->left); // 翻转后的左子树作为新的右子树
root->left = left;
root->right = right;
}
return root;
}
};
解法二:迭代(层序遍历)
class Solution {
public:
TreeNode *invertTree(TreeNode *root) {
queue<TreeNode *> q;
if (root != nullptr)
q.push(root);
while (!q.empty()) {
int size = q.size();
while (size--) {
TreeNode *p = q.front();
q.pop();
swap(p->left, p->right); // 交换所遍历到结点的左右子树
if (p->left)
q.push(p->left);
if (p->right)
q.push(p->right);
}
}
return root;
}
};
5. 对称二叉树 ※
检查二叉树 root 是否轴对称。(101. 对称二叉树)
算法思路:如果一棵树的左右子树互为镜像,那么这棵树是对称的。问题转化为判断两棵树是否互为镜像。
- 两树均为空时,互为镜像。
- 一棵树为空,另一棵树非空时,不互为镜像。
- 两树均非空时,若当两树的外侧子树和内侧子树均互为镜像,且根结点值相同时,互为镜像。
因此,可以实现一个递归函数,通过同步移动两个指针的方法来遍历这棵树,每各移动一次进行一次检查。
class Solution {
public:
bool check(TreeNode *p, TreeNode *q) { // 检查以p为根的子树和以q为根的子树是否互为镜像
if (!p && !q) // 两树均为空,互为镜像
return true;
if (!p || !q) // 一树空一树不空,不互为镜像
return false;
return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);
// 两树均不为空,当两树的外侧子树和内侧子树均互为镜像,且根结点值相同时,两树互为镜像
}
bool isSymmetric(TreeNode *root) {
return check(root->left, root->right);
}
};
6. 二叉树的最大深度
解法一:递归
class Solution {
public:
int maxDepth(TreeNode *root) {
if (root == nullptr)
return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
};
解法二:迭代(层序遍历)
class Solution {
public:
int maxDepth(TreeNode *root) {
queue<TreeNode *> q;
int depth = 0; // 深度
if (root != nullptr)
q.push(root);
while (!q.empty()) {
int size = q.size();
while (size--) {
TreeNode *p = q.front();
q.pop();
if (p->left)
q.push(p->left);
if (p->right)
q.push(p->right);
}
depth++;
}
return depth;
}
};
7. 二叉树的最小深度 ※
求二叉树最浅叶结点的深度。(111. 二叉树的最小深度)
解法一:递归
- 当 root 结点左右孩子都为空时,返回 1。
- 当 root 结点左右孩子有一个为空时,返回不为空的孩子结点的深度+1。
- 当 root 结点左右孩子都不为空时,返回左右孩子较小深度节点的深度+1。
class Solution {
public:
int minDepth(TreeNode *root) {
if (root == nullptr)
return 0;
if (root->left != nullptr && root->right == nullptr)
return minDepth(root->left) + 1;
if (root->left == nullptr && root->right != nullptr)
return minDepth(root->right) + 1;
return min(minDepth(root->left), minDepth(root->right)) + 1;
}
};
解法二:迭代(层序遍历)
class Solution {
public:
int minDepth(TreeNode *root) {
queue<TreeNode *> q;
int depth = 0;
if (root != nullptr)
q.push(root);
while (!q.empty()) {
int size = q.size();
depth++;
while (size--) {
TreeNode *p = q.front();
q.pop();
if (!p->left && !p->right)
return depth; // 若遇到叶结点,直接返回当前深度
if (p->left)
q.push(p->left);
if (p->right)
q.push(p->right);
}
}
return depth;
}
};
8. 完全二叉树的结点个数 ※
递归逻辑:树的结点个数 = 左子树的结点个数 + 右子树的结点个数 + 1。
对完全二叉树而言,分两种情况:
该树是一棵满二叉树,结点个数 = 2^树高^ - 1。(终止条件)
该树底层未满,此时分别递归左右子树,递归到一定深度时总能找到某棵子树为满二叉树,转为情况1。
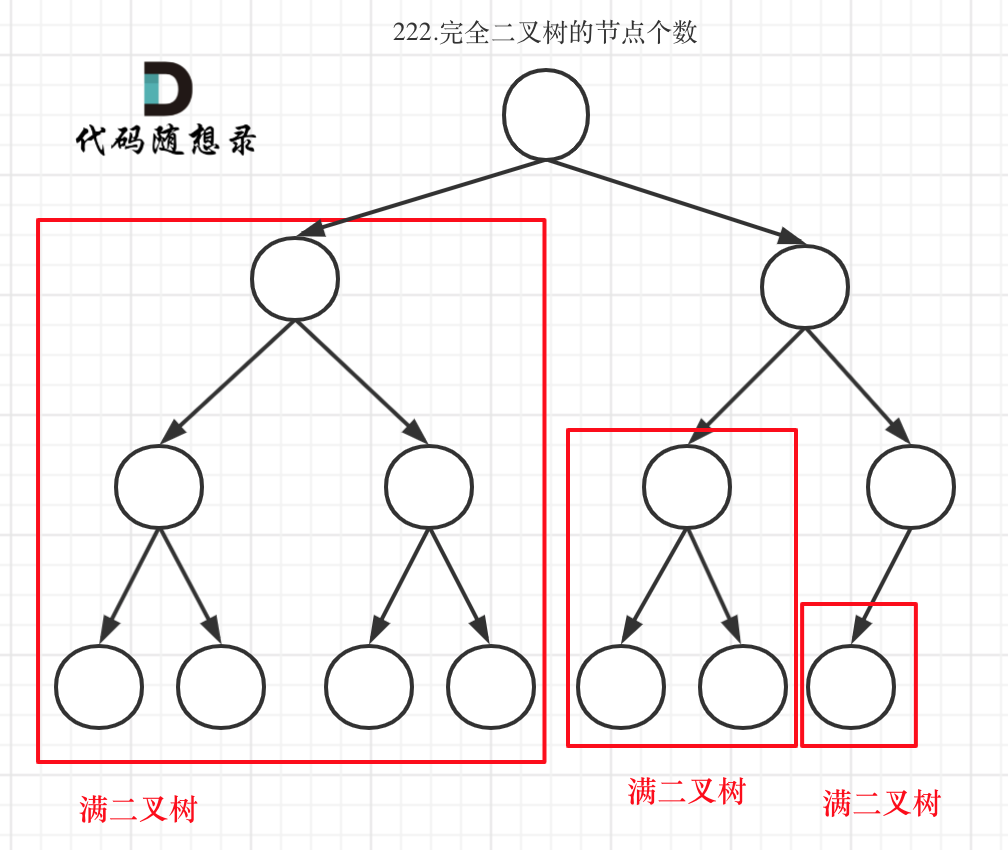
至于如何判断某棵子树是否是满二叉树,根据完全二叉树的性质,如果一路向左遍历的深度等于一路向右遍历的深度,则它是一棵满二叉树。整个算法的时间复杂度为 O(log2 n)。
class Solution {
public:
int countNodes(TreeNode *root) {
int leftDepth = 0, rightDepth = 0;
for (TreeNode *p = root; p != nullptr; p = p->left)
leftDepth++;
for (TreeNode *q = root; q != nullptr; q = q->right)
rightDepth++;
if (leftDepth == rightDepth) // 该完全二叉树是一棵满二叉树
return (1 << leftDepth) - 1; // 2^h-1
return countNodes(root->left) + countNodes(root->right) + 1;
}
};
9. 平衡二叉树 ※
判断一棵树是不是平衡二叉树,即所有结点的左右子树的高度相差不超过 1。(110. 平衡二叉树)
算法思想:自底向上的递归(类似于后序遍历)
对于当前遍历到的结点,先递归地判断其左右子树是否平衡,再判断以当前结点为根的子树是否平衡。如果一棵子树是平衡的,则返回其高度,否则返回 −1。时间复杂度为 O(n)。
class Solution {
public:
int getHeight(TreeNode *root) { // 返回结点的高度,若不是平衡二叉树返回-1
if (root == nullptr)
return 0;
int leftHeight = getHeight(root->left), rightHeight = getHeight(root->right);
if (leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1)
return -1;
return max(leftHeight, rightHeight) + 1;
}
bool isBalanced(TreeNode *root) {
return getHeight(root) != -1;
}
};
29.二叉搜索树中的插入操作 ※
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。
class Solution {
public:
TreeNode *insertIntoBST(TreeNode *root, int val) {
if (root == nullptr)
return new TreeNode(val);
if (val < root->val)
root->left = insertIntoBST(root->left, val);
if (val > root->val)
root->right = insertIntoBST(root->right, val);
return root;
}
};
回溯
回溯算法模板:
void backtracking(参数) { if (剪枝条件) // 可有可无,根据是否剪枝而定 return; if (终止条件) { 存放结果; return; } for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { 处理节点; backtracking(路径,选择列表); // 递归 回溯,撤销处理结果; } }
1. 组合问题 ※
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。(77. 组合)
![]()
class Solution {
public:
vector<vector<int>> combine(int n, int k) {
backtracking(n, k, 1);
return result;
}
private:
vector<vector<int>> result;
vector<int> path; // 存放符合条件结果
void backtracking(int n, int k, int startIndex) { // startIndex记录本层递归搜索的起始位置
if (path.size() == k) { // 终止条件
result.push_back(path);
return;
}
for (int i = startIndex; i <= n; i++) { // for循环: 控制树的横向遍历
path.push_back(i);
backtracking(n, k, i + 1); // 递归: 控制树的纵向遍历,注意下一层搜索要从i+1开始
path.pop_back(); // 回溯
}
}
};
2. 组合总和III
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。(216. 组合总和 III)
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
![]()
class Solution {
public:
vector<vector<int>> combinationSum3(int k, int n) {
backtracking(k, n, 0, 1);
return result;
}
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(int k, int n, int sum, int startIndex) { // sum表示已经收集的元素的总和
if (sum > n) // 剪枝
return;
if (path.size() == k) { // k限制了树的深度
if (sum == n)
result.push_back(path);
return;
}
for (int i = startIndex; i <= 9; i++) {
sum += i;
path.push_back(i);
backtracking(k, n, sum, i + 1);
sum -= i;
path.pop_back();
}
}
};
4. 组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。(39. 组合总和)
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
注意与上题的区别,本题对组合内元素个数没有要求,所以递归没有层数的限制!
![]()
class Solution {
public:
vector<vector<int>> combinationSum(vector<int> &candidates, int target) {
backtracking(candidates, target, 0, 0);
return result;
}
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int> &candidates, int target, int sum, int startIndex) {
if (sum > target) // 剪枝
return;
if (sum == target) {
result.push_back(path);
return;
}
for (int i = startIndex; i < candidates.size(); i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i); // 不用i+1,因为candidates中的同一个数字可以无限制重复被选取
sum -= candidates[i];
path.pop_back();
}
}
};
8. 子集问题
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集。解集不能包含重复的子集。(78. 子集)
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
![]()
class Solution {
public:
vector<vector<int>> subsets(vector<int> &nums) {
backtracking(nums, 0);
return result;
}
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int> &nums, int startIndex) {
result.push_back(path); // 处理空集
if (startIndex >= nums.size()) // 剩余集合为空,到达叶结点
return;
for (int i = startIndex; i < nums.size(); i++) {
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
};
11. 全排列
给定一个不含重复数字的数组 nums,返回其所有可能的全排列。(46. 全排列)
![]()
注意排列问题与组合问题在实现上的不同:
- 每层都从 0 开始搜索,而不是 startIndex;
- 需要一个 used 数组 记录当前 path 中已有哪些元素。
class Solution {
public:
vector<vector<int>> permute(vector<int> &nums) {
vector<bool> used(nums.size(), false); // used数组记录当前path中已有哪些元素
backtracking(nums, used);
return result;
}
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int> &nums, vector<bool> &used) {
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) { // 每层都从0开始搜索,而不是startIndex
if (used[i]) // path中已有该元素,直接跳过
continue;
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
used[i] = false;
path.pop_back();
}
}
};
动态规划
1. 斐波那契数
F 是斐波那契数列,计算 F(n)。(509. 斐波那契数)
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
class Solution {
public:
int fib(int n) {
if (n <= 1)
return n;
vector<int> dp(n + 1);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[n];
}
};
2. 最长递增子序列
给你一个整数数组 nums,找到其中最长严格递增子序列的长度。
算法思想:
dp[i]:以 nums[i] 结尾的最长递增子序列的长度。状态转移方程:
nums[0 .. i]的最长递增子序列等于 j 从 0 到 i - 1 各个位置的最长递增子序列 + 1 的最大值。for (int j = 0; j < i; j++) if (nums[j] < nums[i]) dp[i] = max(dp[i], dp[j] + 1);初始化:
for (int i = 0; i < n; i++) dp[i] = 1;
class Solution {
public:
int lengthOfLIS(vector<int> &nums) {
int result = 1;
vector<int> dp(nums.size(), 1);
for (int i = 1; i < nums.size(); i++)
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i])
dp[i] = max(dp[i], dp[j] + 1);
result = max(result, dp[i]);
}
return result;
}
};
3. 最长连续递增序列
给定一个未经排序的整数数组,找到最长且连续递增的子序列,并返回该序列的长度。
算法思想:
dp[i]:以 nums[i] 结尾的连续递增的子序列的长度。- 状态转移方程:
if (nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1; - 初始化:
for (int i = 0; i < n; i++) dp[i] = 1;
class Solution {
public:
int findLengthOfLCIS(vector<int> &nums) {
int result = 1;
vector<int> dp(nums.size(), 1);
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > nums[i - 1])
dp[i] = dp[i - 1] + 1;
result = max(result, dp[i]);
}
return result;
}
};
4. 最长重复子数组
给两个整数数组 A 和 B,返回两个数组中公共的、长度最长的子数组的长度。
算法思想:
dp[i][j]:A[0 .. i - 1]和B[0 .. j - 1]的最长重复子数组长度。- 状态转移方程:当
A[i - 1] == B[j - 1]时,dp[i][j] = dp[i - 1][j - 1] + 1。 - 初始化:
dp[i][0] = dp[0][j] = 0。
class Solution {
public:
int findLength(vector<int> &nums1, vector<int> &nums2) {
vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1));
int result = 0;
for (int i = 1; i <= nums1.size(); i++)
for (int j = 1; j <= nums2.size(); j++) {
if (nums1[i - 1] == nums2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
result = max(result, dp[i][j]);
}
return result;
}
};
5. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
输入:text1 = "abcde", text2 = "ace"
输出:3
算法思想:
dp[i][j]:text1[0 .. i - 1]和text2[0 .. j - 1]的最长公共子序列长度。状态转移方程:
if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1; else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);初始化:
dp[i][0] = dp[0][j] = 0。
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1));
for (int i = 1; i <= text1.size(); i++)
for (int j = 1; j <= text2.size(); j++) {
if (text1[i - 1] == text2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
return dp[text1.size()][text2.size()];
}
};
6. 最大子序和
给你一个整数数组 nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
算法思想:
dp[i]:以 nums[i] 结尾的最大连续子序列的和- 状态转移方程:
dp[i] = max(dp[i - 1] + nums[i], nums[i]); - 初始化:
dp[0] = nums[0]。
class Solution {
public:
int maxSubArray(vector<int> &nums) {
vector<int> dp(nums.size());
int result = dp[0] = nums[0];
for (int i = 1; i < nums.size(); i++) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
result = max(result, dp[i]);
}
return result;
}
};
7. 最长回文子序列
给你一个字符串 s,找出其中最长的回文子序列,并返回该序列的长度。
输入:s = "bbbab"
输出:4
dp[i][j]:s[i..j]的最长回文子序列的长度。状态转移方程:
if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2; else dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);初始化:
dp[i][i] = 1。
class Solution {
public:
int longestPalindromeSubseq(string s) {
vector<vector<int>> dp(s.size(), vector<int>(s.size()));
for (int i = 0; i < s.size(); i++)
dp[i][i] = 1;
for (int i = s.size() - 1; i >= 0; i--) // i从下向上遍历
for (int j = i + 1; j < s.size(); j++)
if (s[i] == s[j])
dp[i][j] = dp[i + 1][j - 1] + 2;
else
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
return dp[0][s.size() - 1];
}
};
图论
DFS 模板:
void dfs(参数) { if (终止条件) { 存放结果; return; } for (选择:本节点所连接的其他节点) { 处理节点; dfs(图,选择的节点); // 递归 回溯,撤销处理结果 } }邻接矩阵及其构造方式:
vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0)); while (m--) { cin >> s >> t; graph[s][t] = 1; // 顶点s指向顶点t }邻接表及其构造方式:
vector<list<int>> graph(n + 1); while (m--) { cin >> s >> t; graph[s].push_back(t); // 顶点s指向顶点t }
1. 所有可达路径 ※
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个程序,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。(98. 所有可达路径 - 卡码网KamaCoder)
输入描述:
第一行包含两个整数 N,M,表示图中拥有 N 个节点,M 条边
后续 M 行,每行包含两个整数 s 和 t,表示图中的 s 节点与 t 节点中有一条路径
输入:
5 5
1 3
3 5
1 2
2 4
4 5
输出:
1 3 5
1 2 4 5
邻接矩阵实现:
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> result;
vector<int> path;
void dfs(const vector<vector<int>> &graph, int x, int n) { // x表示目前遍历到的结点,n表示终点
if (x == n) {
result.push_back(path);
return;
}
for (int i = 1; i <= n; i++) {
if (graph[x][i] == 1) {
path.push_back(i);
dfs(graph, i, n);
path.pop_back();
}
}
}
int main() {
int m, n, s, t; // m条边,n个顶点
cin >> n >> m;
vector<vector<int>> graph(n + 1, vector<int>(n + 1)); // 邻接矩阵
while (m--) {
cin >> s >> t;
graph[s][t] = 1;
}
path.push_back(1);
dfs(graph, 1, n);
if (result.size() == 0)
cout << -1 << endl; // 不存在任何一条路径,输出-1
for (vector<int> &v : result) {
for (size_t i = 0; i < v.size() - 1; i++)
cout << v[i] << ' ';
cout << v[v.size() - 1] << endl;
}
}
邻接表实现:
#include <iostream>
#include <list>
#include <vector>
using namespace std;
vector<vector<int>> result;
vector<int> path;
void dfs(const vector<list<int>> &graph, int x, int n) { // x表示目前遍历到的结点,n表示终点
if (x == n) {
result.push_back(path);
return;
}
for (int i : graph[x]) {
path.push_back(i);
dfs(graph, i, n);
path.pop_back();
}
}
int main() {
int m, n, s, t; // m条边,n个顶点
cin >> n >> m;
vector<list<int>> graph(n + 1); // 邻接表
while (m--) {
cin >> s >> t;
graph[s].push_back(t);
}
path.push_back(1);
dfs(graph, 1, n);
if (result.size() == 0)
cout << -1 << endl; // 不存在任何一条路径,输出-1
for (vector<int> &v : result) {
for (size_t i = 0; i < v.size() - 1; i++)
cout << v[i] << ' ';
cout << v[v.size() - 1] << endl;
}
}
3. Floyd 算法
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。请你帮助小明计算出每个观景计划的最短路径长度。
### 输入描述
第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。
接下来的 M 行,每行包含三个整数 u, v, w,表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。
接下里的一行包含一个整数 Q,表示观景计划的数量。
接下来的 Q 行,每行包含两个整数 start, end,表示一个观景计划的起点和终点。
### 输出描述
对于每个观景计划,输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径,则输出 -1。
### 输入示例
7 3
2 3 4
3 6 6
4 7 8
2
2 3
3 4
### 输出示例
4
-1
### 提示信息
从 2 到 3 的路径长度为 4,3 到 4 之间并没有道路。
1 <= N, M, Q <= 1000.
1 <= w <= 10000.
#include <iostream>
#include <vector>
using namespace std;
int main() {
int m, n, u, v, w, q, start, end;
cin >> n >> m;
vector<vector<int>> grid(n + 1, vector<int>(n + 1, 10001)); // grid[i][j]存放顶点i到顶点j的最短路径长度
while (m--) {
cin >> u >> v >> w;
grid[u][v] = w;
grid[v][u] = w;
}
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);
cin >> q;
while (q--) {
cin >> start >> end;
cout << (grid[start][end] == 10001 ? -1 : grid[start][end]) << endl;
}
}
